Question

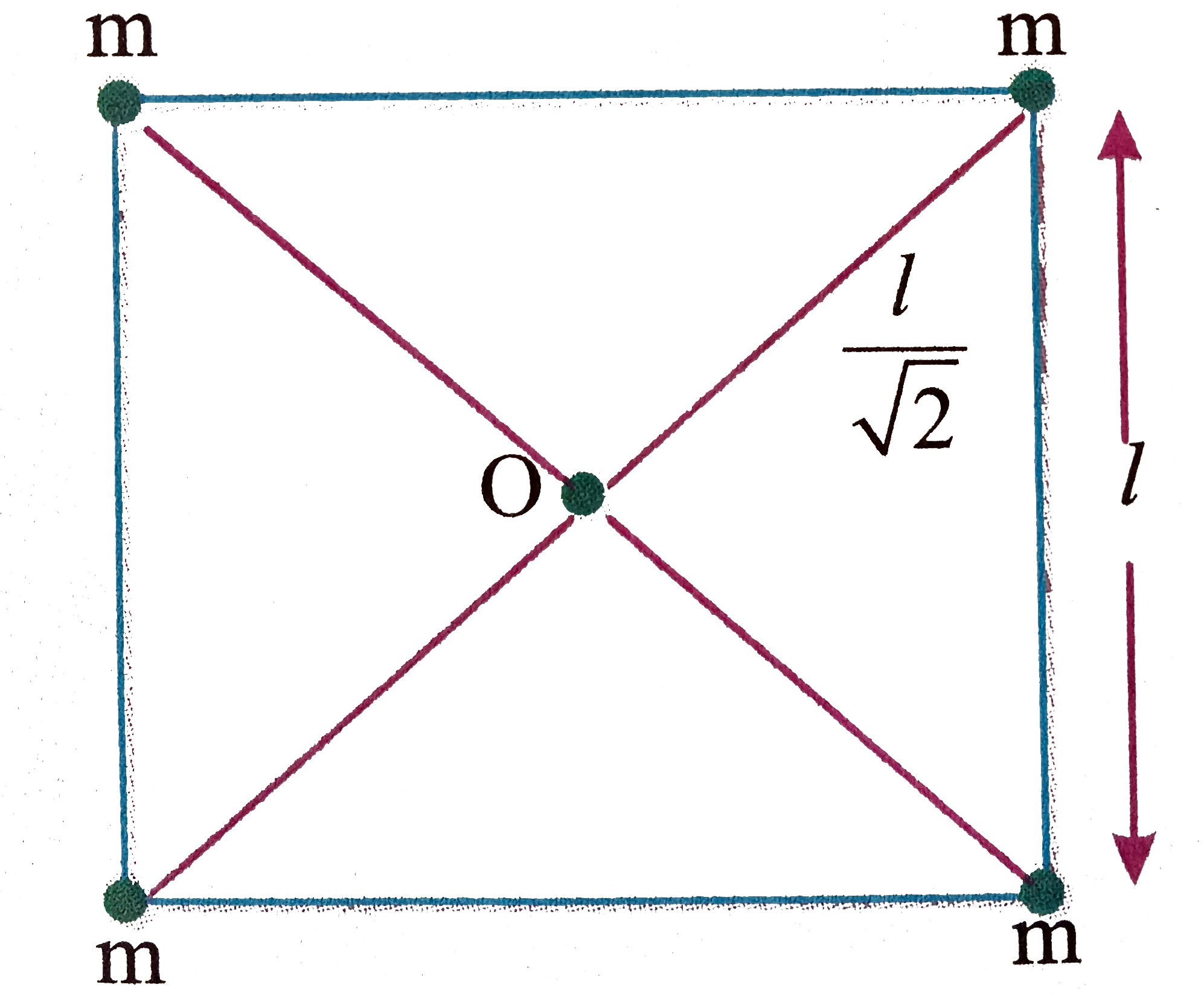
Four identical particles of mass "m" are kept at the four corners of a square.If the gravitational force exerted on one of the masses by the other masses is $\left(\frac{2\sqrt{2}+1}{32}\right)\frac{G{m}^2}{L^2}$, the length of the sides of the square is

Options

A. 2L
B. 4L
C. `L/2`
D. 3L

Answer

B

Explanation

To solve the problem, we need to find the length of the sides of a square (denoted as $$L$$) given the gravitational force exerted on one of the masses by the other masses.

1. Understanding the Setup:
- We have four identical particles, each of mass \( m \), located at the corners of a square. The side length of the square is \( L \).

2. Gravitational Force Between Two Particles:
- The gravitational force \( F \) between any two masses \( m \) separated by a distance \( r \) is given by Newton's law of gravitation:
\( F = \frac{G m_1 m_2}{r^2} \)
- For the particles at the corners of the square, we will consider the forces acting on one particle due to the other three particles.

3. Calculating Forces:
- Let’s denote the corners of the square as \( A, B, C, D \). We will calculate the forces acting on mass at corner \( A \).
- The distance between \( A \) and \( B \) (adjacent corner) is \( L \).
- The distance between \( A \) and \( C \) (diagonal corner) is \( \sqrt{2}L \).

4. Force from Adjacent Corners:
- The gravitational force between \( A \) and \( B \):
\( F_{AB} = \frac{G m^2}{L^2} \)
- The gravitational force between \( A \) and \( D \):
\( F_{AD} = \frac{G m^2}{L^2} \)

5. Force from Diagonal Corner:
- The gravitational force between \( A \) and \( C \):
\( F_{AC} = \frac{G m^2}{(\sqrt{2}L)^2} = \frac{G m^2}{2L^2} \)

6. Net Force Calculation:
- The forces \( F_{AB} \) and \( F_{AD} \) act along the sides of the square, while \( F_{AC} \) acts diagonally.
- The net force \( F_{net} \) on mass \( A \) can be calculated using vector addition:
- The components of \( F_{AB} \) and \( F_{AD} \) can be added directly since they are along the axes.
- The diagonal force \( F_{AC} \) needs to be resolved into its components.

7. Resolving Forces:
- The components of \( F_{AC} \):
\( F_{ACx} = F_{AC} \cdot \cos(45^\circ) = \frac{G m^2}{2L^2} \cdot \frac{1}{\sqrt{2}} = \frac{G m^2}{2\sqrt{2}L^2} \)
\( F_{ACy} = F_{AC} \cdot \sin(45^\circ) = \frac{G m^2}{2L^2} \cdot \frac{1}{\sqrt{2}} = \frac{G m^2}{2\sqrt{2}L^2} \)

8. Total Net Force:
- The total force in the x-direction:
\( F_{net,x} = F_{AB} + F_{ACx} = \frac{G m^2}{L^2} + \frac{G m^2}{2\sqrt{2}L^2} \)
- The total force in the y-direction:
\( F_{net,y} = F_{AD} + F_{ACy} = \frac{G m^2}{L^2} + \frac{G m^2}{2\sqrt{2}L^2} \)

9. Magnitude of the Net Force:
- The magnitude of the net force can be calculated using the Pythagorean theorem:
\( F_{net} = \sqrt{(F_{net,x})^2 + (F_{net,y})^2} \)

10. Setting Equal to Given Force:
- We know from the problem that:
\( F_{net} = \frac{(2\sqrt{2}+1)}{32} \frac{G m^2}{L^2} \)
- By equating and simplifying, we can solve for \( L \).

Final Calculation:
After performing the calculations and simplifications, we can find the length \( L \) of the sides of the square.