If the tangent at a point on the ellipse x227+y23=1 meets the coordinate axes at A and B, and the origin, then the minimum area (in sq. units) of the triangle OAB is:
3√3
92
9
9√3
The correct Answer is:C
Step by step video & text solution for If the tangent at a point on the ellipse x^2/27+y^2/3=1 meets the coordinate axes at A and B, and the origin, then the minimum area (in sq. units) of the triangle OAB is: by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
If the length of sub-normal is equal to the length of sub-tangent at any point (3,4) on the curve y=f(x) and the tangent at (3,4) to y=f(x) meets the coordinate axes at AandB , then the maximum area of the triangle OAB, where O is origin, is 45/2 (b) 49/2 (c) 25/2 (d) 81/2
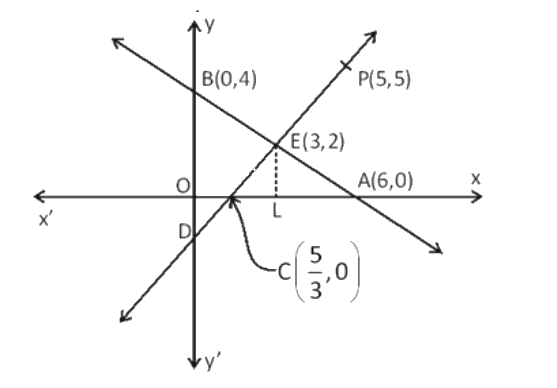
View SolutionThe line 2x+3y=12 meets the coordinates axes at A and B respectively. The line through (5, 5) perpendicular to AB meets the coordinate axes and the line AB at C, D and E respectively. If O is the origin, then the area (in sq. units) of the figure OCEB is equal to
View Solution
Knowledge Check
The tangent and normal to the ellipse 3x2+5y2=32 at the point P(2, 2) meet the x-axis at Q and R, respectively. Then the area (in sq. units) of the triangle PQR is:
A3415B163C6815D143Any tangent at a point P(x,y) to the ellipse x28+(y2)=1 meets the coordinate axes in the points A and B such that the area of the triangle OAB is least, then the point P is
A(√8,0)B(0,√18)C(2,3)DnoneTangent at a point on the ellipse x2a2+y2b2=1
is drawn which cuts the coordinates axes at A and B the maximum area of the triangle OAB is ( O being origin )AabBa3+b3+ab3Ca2+b2Da2+b24
A tangent having slope −43 to the ellipse x218+y232=1 intersects the major and minor axes at A and B .If o is origin,then the area of ,ΔOAB is k sq.units where sum of digits of k is
View SolutionIf the plane x1+y2+z3=1 meets the co-ordinate axes in the points A, B and C, then area of △ABC in sq. units is
View SolutionTangent to the ellipse x232+y218=1 having slope −34 meet the coordinate axes in A and B. Find the area of the △AOB, where O is the origin.
View Solutionthe tangent and normal to the tangent to the ellipse x2a2+y2b2=1 at the point (3,−92), then the area ( in sq units ) of the ΔPQR Is
View SolutionTangent to the ellipse x232+y218=1 having slope −34 meet the coordinates axes in A and B. Find the area of the ΔAOB , where O is the origin .
View Solution
