For the reaction $A \to$ Product
$k = \frac{1}{t} [\frac{1}{a - x} - \frac{1}{a}]$
Where k is rate constant (in $m o l^{- 1} s^{- 1}$ ) and $(a - x)$ are the concentration of A at the start and after time interval t sec. A graph between $\frac{1}{a - x}$ and time t is of the following

A

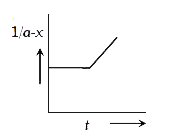
ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:C

To solve the problem, we start with the given equation for the reaction:
$k = \frac{1}{t} (\frac{1}{a - x} - \frac{1}{a})$
Where:
- $k$ is the rate constant (in ${mol}^{- 1} s^{- 1}$ ),
- $a$ is the initial concentration of reactant A,
- $x$ is the amount of A that has reacted after time $t$ .
Step 1: Rearranging the Equation
We can rearrange the equation to express $\frac{1}{a - x}$ in terms of $t$ :
$k t = \frac{1}{a - x} - \frac{1}{a}$
Adding $\frac{1}{a}$ to both sides gives:
$\frac{1}{a - x} = k t + \frac{1}{a}$
Step 2: Identifying the Linear Form
This equation can be compared to the linear equation $y = m x + c$ , where:
- $y = \frac{1}{a - x}$ ,
- $m = k$ (the slope),
- $x = t$ (the independent variable),
- $c = \frac{1}{a}$ (the y-intercept).
Step 3: Analyzing the Graph
From the rearranged equation, we can conclude:
- The graph of $\frac{1}{a - x}$ versus $t$ is a straight line.
- The slope of this line is positive since $k$ is a positive rate constant.
- The y-intercept is $\frac{1}{a}$ .
Step 4: Evaluating the Options
Now, we need to evaluate the given options for the graph:
1. A graph with a negative slope is incorrect because $k$ is positive.
2. A graph with a zero slope is incorrect because $k$ is not zero.
3. A graph with a positive slope and a y-intercept of $\frac{1}{a}$ is correct.
4. A graph with a zero slope is again incorrect.
Thus, the correct option is the one that shows a straight line with a positive slope and a y-intercept at $\frac{1}{a}$ .
Conclusion
The graph of $\frac{1}{a - x}$ versus time $t$ will be a straight line with a positive slope $k$ and a y-intercept of $\frac{1}{a}$ .

Updated on:8/8/2024

|

Class 12 CHEMISTRY CHEMICAL KINETICS

Similar Questions

Knowledge Check

Given that for a reaction of order n, the integrated from of the rate equation is :
$k = \frac{1}{t (n -)} [\frac{10}{C^{n - 1}} - \frac{1}{C_{0}^{n - 1}}]$ where $C_{0}$ and C are the values of the reactant concentration at the start and after tme t. What is the relationship between $t_{3 / 4}$ and $t_{1 / 2}$ where $t_{3 / 4}$ is the time required for C to become $\frac{1}{4} C_{0}$ ?
A $t_{3 / 4} = t_{1 / 2} [2^{n - 1} + 1]$
B $t_{3 / 4} = t_{1 / 2} [2^{n - 1} - 1]$
C $t_{3 / 4} = t_{1 / 2} [2^{n + 1} - 1]$
D $t_{3 / 4} = t_{1 / 2} [2^{n + 1} + 1]$
Given that for a reaction of nth order, the integrated rate equation is:
$K = \frac{1}{t (n - 1)} [\frac{1}{C^{n - 1}} - \frac{1}{C_{0}^{n - 1}}]$ , where $C$ and $C_{0}$ are the concentration of reactant at time $t$ and initially respectively. The $t_{3 / 4}$ and $t_{1 / 2}$ are related as $t_{3 / 4}$ is time required for C to become $C_{1 / 4}$ ) :
A $t_{3 / 4} = t_{1 \frac{/}{2}} [2^{n - 1} + 1]$
B $t_{3 / 4} = t_{1 \frac{/}{2}} [2^{n - 1} - 1]$
C $t_{3 / 4} = t_{1 \frac{/}{2}} [2^{n - 1} - 1]$
D $t_{3 / 4} = t_{1 \frac{/}{2}} [2^{n + 1} + 1]$
Graph between log k and $1 / T$ [where K is rate constant in $s^{- 1}$ and T is the temperature (in K) is a straight line with Hence, $E_{a}$ will be

A $2.303 \times 2$ cal
B $\frac{2}{2.303} c a l$
C2 cal
DNone of these

Recommended Questions

Home
Ask Doubt
Profile