Consider a Young's double slit experiment as shown in figure. What would be the slit separation d in terms of wavelength λ such that the first minima occurs directly in front of the (S1) ?

λ(√5−2)
λ2(5−√2)
λ2(√5−2)
λ(5−√2)
The correct Answer is:C
x1=2d
x2=√5d
Δx=x2−x1
√5d−2d=λ2⇒d=λ2(√5−2)
Similar Questions
Knowledge Check
In Young's double slit experiment, if the widths of the slits are in the ratio 4:9, the ratio of the intensity at maxima to the intensity at minima will be
A169:25B81:16C25:1D9:4In Young's double slit experiment, if the widths of the slits are in the ratio 4:9, the ratio of the intensity at maxima to the intensity at minima will be
A169:25B81:16C25:1D9:4White light is used to illuminate the two slits in a Young's double slit experiment. The separation between the slits is b and the screen is at a distance d(gtb) from the slits. At a point on the screen directly in front of one of the slits, certain wavelength are missing. Some of these missing wavelength are
Aλ=b2dBλ=2b2dCλ=b23dDλ=2b23d
In Young's double slit experiment interference fringes 1∘ apart are produced on the screen, the slit separation is (λ=589nm)
View Solution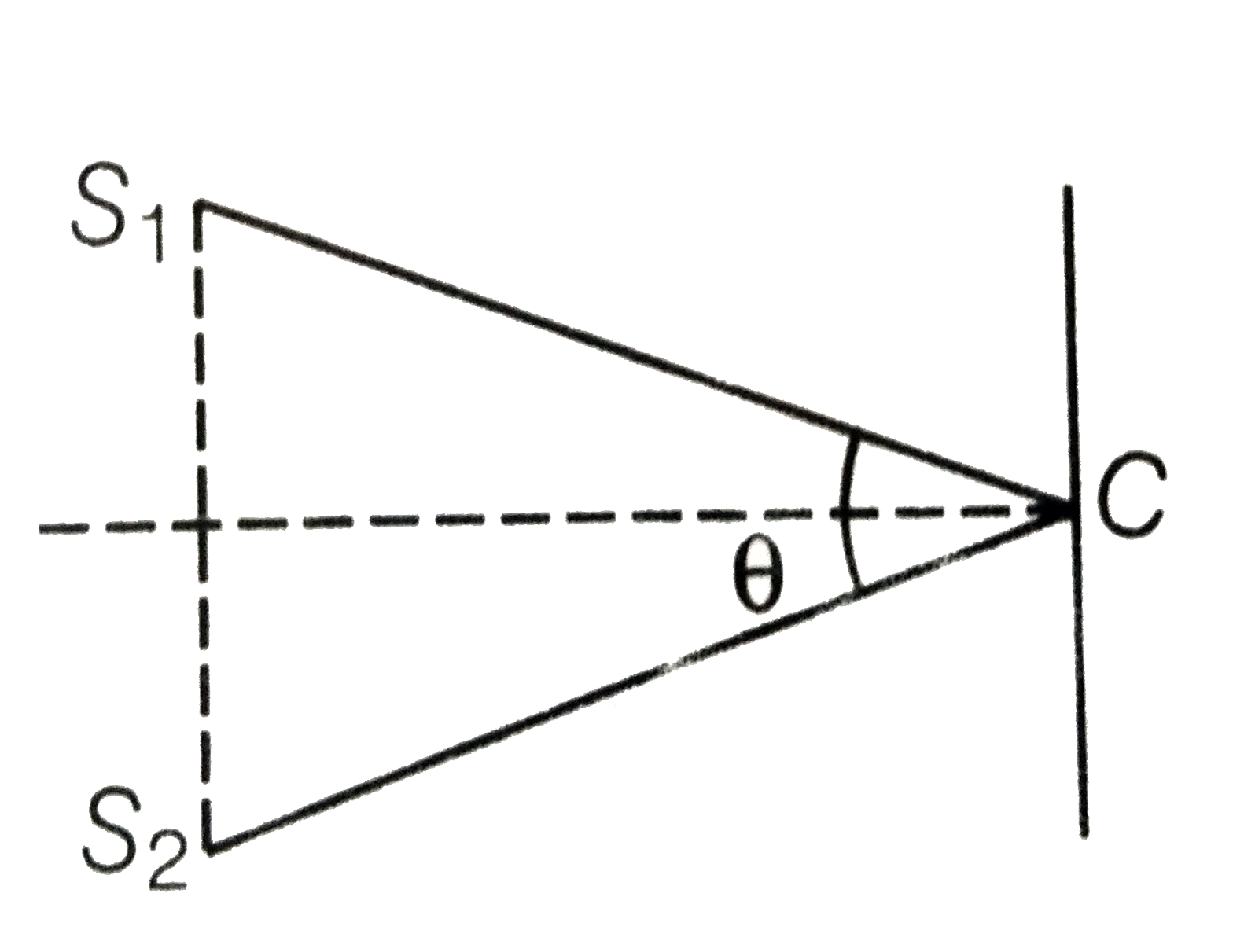
Young's double slit experimental arrangement is shown in figure. If λ is the wavelength of light used and ∠S1CS2=θ, then the fringe width will be
View SolutionWhite light is used to illuminate the two slits in a Young's double slit experiment. The separation between the slits is b and the screen is at a distance d(>>b) from the slits At a point on the screen directly in front of one of the slits, certain wavelengths are missing some of these missing wavelengths are
View SolutionIn Young's double slit experiment, if the slit widths are in the ratio 1:9, then the ratio of the intensity at minima to that at maxima will be
View SolutionWhite light is used to illuminate the two slits in a Young's
double slit experiment. The separation between the slits is b and the screen is at
a distance d(>>b) from the slits. At a point on the screen directly in front of
one of the slits, certain wavelengths are missing. Some of these missing
wavelength are
(a)λ=b2/d(b)λ=2b2/d(c)λ=b2/3d(d)λ=2b2/3d .
View Solution
