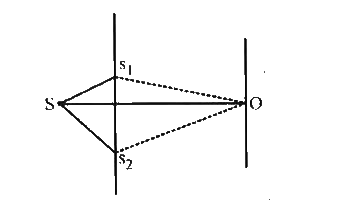
Figure shows a standard two slit arrangement with slits S1,S2.P1,P2 are the two minima points on either side of P (Figure). At P2 on the screen, there is a hole and behind P2 is a second 2-slit arrangement with slits S3,S4 and a second screen behind them.

There would be no interference pattern on the second screen but it would be lighted
The second screen would be totally dark
There would be a single bright point on the second screen
There would be a regular two slit pattern on the second screen
The correct Answer is:D
According to question, there is a hole at point P2 . From Huygen’s principle, wave will propagate from the sources S1 and S2 . Each point on the screen will acts as secondary sources of wavelets. Now, there is a hole at point P2 (minima). The hole will act as a source of fresh light for the slits S3 and S4 . Therefore, there will be a regular two slit pattern on the second screen.
Similar Questions
In an interference experiment, the two slits S1andS2 are not equidistant from the source S. then the central fringe at 0 will be
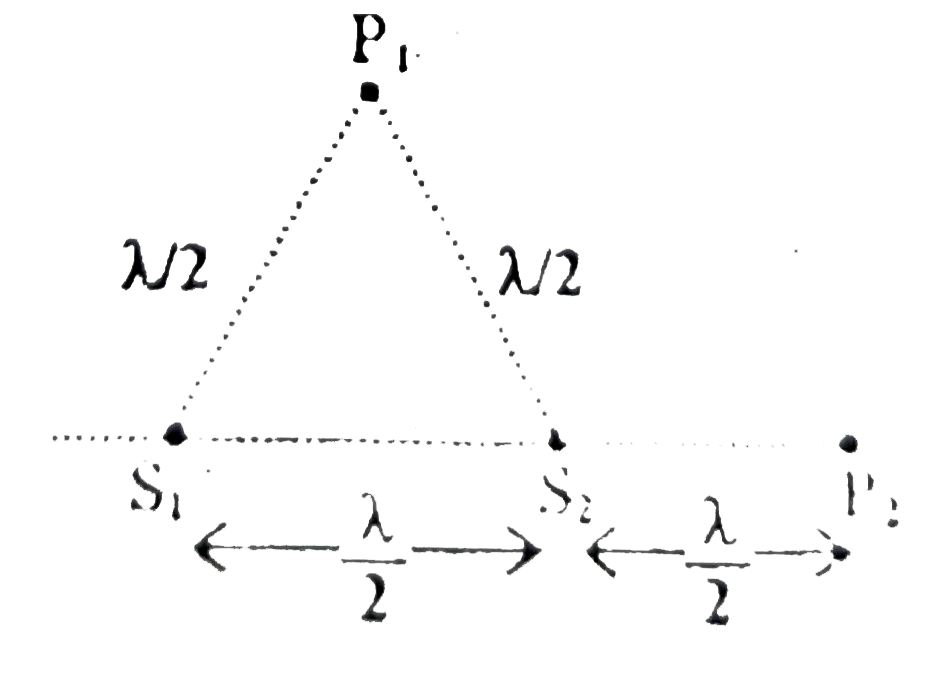
View SolutionS1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be
View Solution
Knowledge Check
In a Young's double slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is the wavelength, the fringe width will be
AλθBλθC2λθDλ2θIn a Young's double-slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is wavelength, the fringe width will be
AλθBλθC2λθDλ2θA coherent light is incident on two paralle slits S1andS2. At a point P1 the frings will be dark if the phase difference between the rays coming from S1andS2 is
Anπ radiansB(n+0.5)π radiansC(2n+0.5)π radiansD(2n+1)π radians
Monochromatic light of wavelength λ passes through a very narrow slit S and then strikes a screen placed at a distance D = 1m in which there are two parallel slits S1 and S2 as shown. Slit S1 is directly in line with S while S2 is displaced a distance d to one side. The light is detected at point P on a second screen, equidistant from S1 and S2 When either slit S1 or S2 is open equal light intensities I are measured at point P. When both slits are open, the intensity is three times as large i.e. 3I. If the minimum possible wavelength is Nd2, then find the value of N(d<<D)

View SolutionIn the arrangement shown in Fig., slits S1 and S4are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of S1S2 and S3S4.
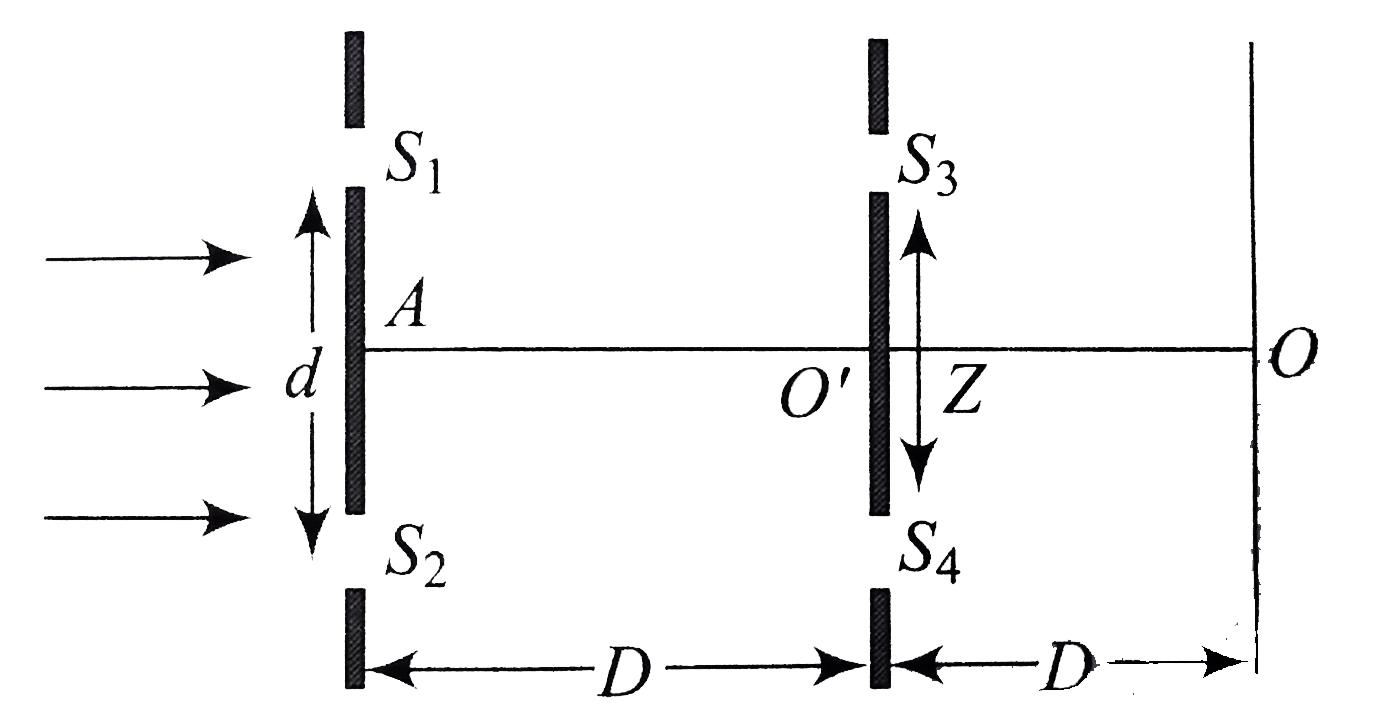
The minimum value of Z for which the intensity at O is zero is
View SolutionIn a Young’s double slit experiment, the separation of the two slits is doubled. To keep the same spacing of fringes, the distance D of the screen from the slits should be made
View Solution_E01_054_Q01.png)
A monochromatic light source of wavelength λ is placed at S. three slits S1,S2 and S3 are equidistant from the source S and the point P on the screen S1P−S2P=λ/6 and S1P−S3P=2λ/3. if I be the intensity at P when only one slit is open the intensity at P when all the three slits are open is-
View SolutionIn Young's double slit experiment, the slits are horizontal. The intensity at a point P as shown in figure is 34I0,where I0 is the maximum intensity.
Then the value of θ is,
(Given the distance between the two slits S1 and S2 is 2λ)

View Solution
