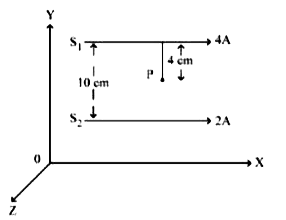
Two long parallel consuctors S1andS2 are separated by a distance 10 cm and carrying of 4A and 2A respectively . The conductors are placed along x axis in X-Y plane . There is a point P located between the conductors (as shown in figure ).
A charge particle of 3π coulomb is passing through the point P with velocity →v=(2ˆi+3ˆj)m/s , where ˆi&ˆj represents unit vector along x & y axis respectively .
The force acting on the charge particle is 4π×10−5(−xˆi+2ˆj)N . The values of x is :
2
1
3
−3
The correct Answer is:C
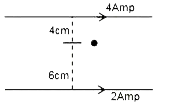
BNet=μ042π×4100−μ022π×6100
=μ0π×100[12−16]
=μ0π×100[42×6]
=μ0×1003π(−ˆk)
→F=9(→V×→B)=3π[2ˆi+3ˆj]μ0×1003π(−ˆk)
=4π×10−7[2ˆi+3ˆj]×100(−ˆk)
=4π×10−5[2ˆj−3ˆi]
∴x=3
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PART : PHYSICS
30 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
Knowledge Check
The angle which the vector →A=2ˆi+3ˆj makes with the y-axis, where ˆi and ˆj are unit vectors along x- and y-axis, respectively, is
Acos−1(3/5)Bcos−1(2/3)Ctan^(-1)(2//3)Dsin−1(2/3)A projectile is given an initial velocity of (ˆi+2ˆj)m/s, where ˆi is along the ground and ˆj is along the vertical . If g=10m/s2, the equation of its trajectory is :
Ay=x−5x2By=2x−5x2C4y=2x−5x2D4y=2x−25x2
A particle of mass 2kg is moving with velocity →v0=(2ˆi−3ˆj)m/s in free space. Find its velocity 3s after a constant force →F=(3ˆi+4ˆj)N starts acting on it.
View SolutionShow that If →a=xˆi+2ˆj−zˆk and →b=3ˆi−yˆj+ˆk are two equal vectors, then x+y+z=0.
View SolutionWrite the vector equation of the plane passing through the point (a,b,c) and parallel to the plane →r.(ˆi+ˆj+ˆk)=2.
View SolutionFind the vector and cartesian equations of the line passing through the point P (1, 2, 3) and parallel to the planes →r.ˆi− ˆj+2ˆk=5 and →r.3ˆi+ˆj+ˆk=6.
View SolutionThe distance of point B with position vector ˆi+2ˆj+3ˆk from the line passing through the point with position vector 4ˆi+2ˆj+2ˆk and parallel to the vector 2ˆi+3ˆj+6ˆk is :
View SolutionThe distance of point B with position vector ˆi+2ˆj+3ˆk from the line passing through the point with position vector 4ˆi+2ˆj+2ˆk and parallel to the vector 2ˆi+3ˆj+6ˆk is :
View Solution
