The circuit is switched on at t=0, Find the time when energy stored in inductor becomes 1n tiimes of maximum energy stored in it: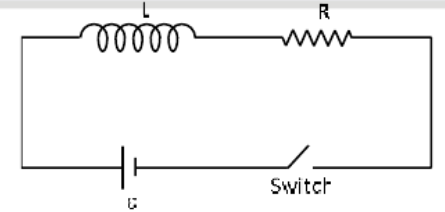
LRln(√n√n−1)
LRln(√n+1√n−1)
LRln(√n√n+1)
LRln(√n−1√n)
The correct Answer is:A
Umax=12LI2max
i=Imax(1−e−Rt/L)
For U to be Umaxn , i has to be Imax√n
Imax√n=Imax(1−eRt/L)
e−Rt/L=1−1√n=√n−1√n
−RtL=ln(√n−1)√n
t=LRln(√n√n−1)
Similar Questions
Energy Stored In An Inductor
View SolutionA charged capacitor is connected to an inductor . At a particular instant, energy stored in inductor is 8/9 times of initial energy stored In capacitor . What is the ratio of initial charge on capacitor to that with instantaneous charge on capacitor ?
View Solution
Knowledge Check
The capacitor shown in the figure is initially unchanged, the battery is ideal. The switch S is closed at time t= 0, then the time after which the energy stored in the capacitor becomes one - fourth of the energy stored in it in steady - state is :
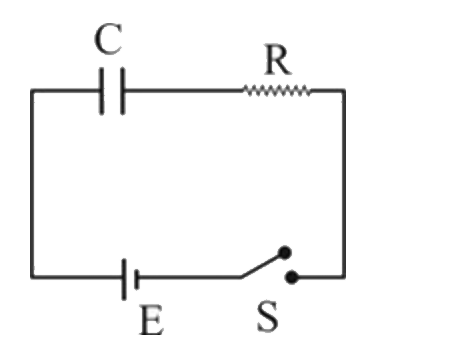 ARCBRC ln 2CRC ln 4D2RC
ARCBRC ln 2CRC ln 4D2RCA simple LR circuit is connected to a battery at time t=0. The energy stored in the inductor reaches half its maximum value at time
ARL In [√2√2−1]BLR In [√2−1√2]CLR In [√2√2−1]DRL In [√2−1√2]In the circuit shown, the energy stored in 1μF capacitor is
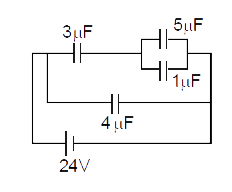 A40μJB64μJC32μJDnone of these
A40μJB64μJC32μJDnone of these
Figure-5.150 shows LC circuit with initial charge on capacitor 200μC. If at t=0 switch is closed, find the first instant when energy stored in inductor becomes one third that of capacitor.

View Solution
At t=0 switch S is closed .
(a) After how much time , charge on capacitor is 50% of maximum charge stored on capacitor.
(b) After how much time, energy stored in capacitor is halt of maximum energy stored in capacitor.
View SolutionA circuit contains 50 μF capacitor and 20 mH inductor connected together with the help of a key which is open initially. Charge stored in the capacitor is 50 mC. Key is closed at t=0 . Calculate the minimum time interval in which energy stored in the inductor becomes equal to the energy stored in capacitor . Neglect any resistance in the circuit .
View SolutionIn the steady state of the circuit shown in the figure the ratio of energy stored in the inductor to th energy stored in the capacitor is 10000.

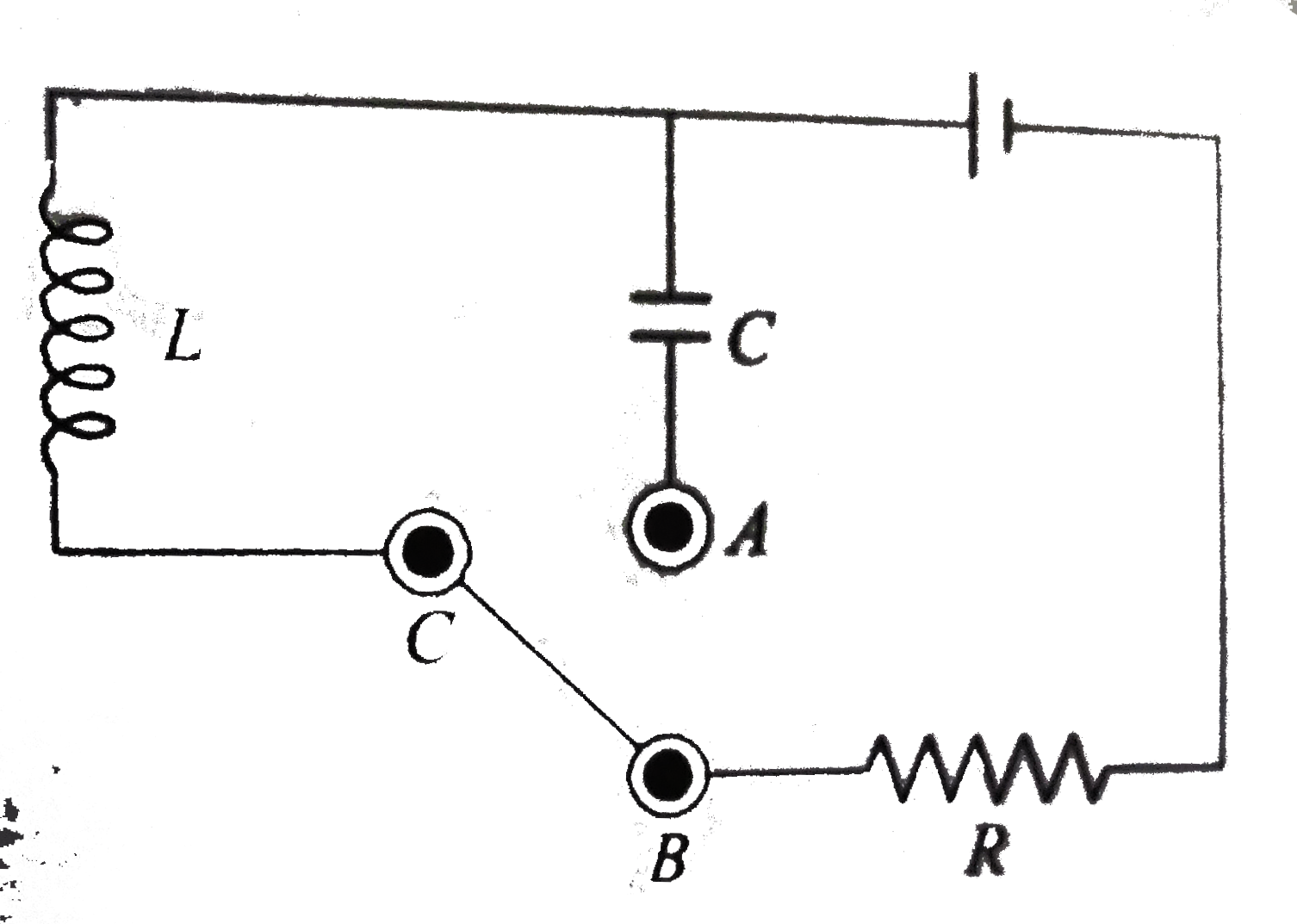
View SolutionIn the circuit shows in Fig the capacitor is initially uncharged and the two - way switch is connected in the position BC. Find the current through the resistence R as a function of time t. After time t=4 ms, the switch is connected in the position AC. Find the frequency of oscillation of the capacitor of the circuit in the position, and the maximum charge on the capacitor C. At what time will the energy stored in the capacitor be one-half of the total energy stored in the circuit? It is given L=2×10−4H,C=5mF,R=In210Ω and emf of the battery =1V.
View Solution
