When an AC source of is connected across a circuit i in the circuit, the phase difference between the emf e and the current i in the circuit is observed to be , as shown in the diagram. If the circuit consists possibly only of R-C or R-L or L-C in series, find the relationship between the two elements
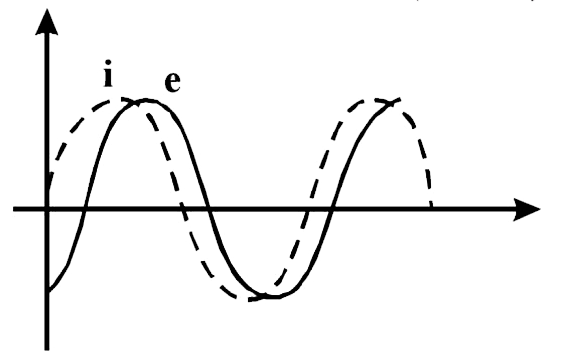
The correct Answer is:A
Since, current leads voltage,
Then for capacitive circuit here
Now, from the options
Similar Questions
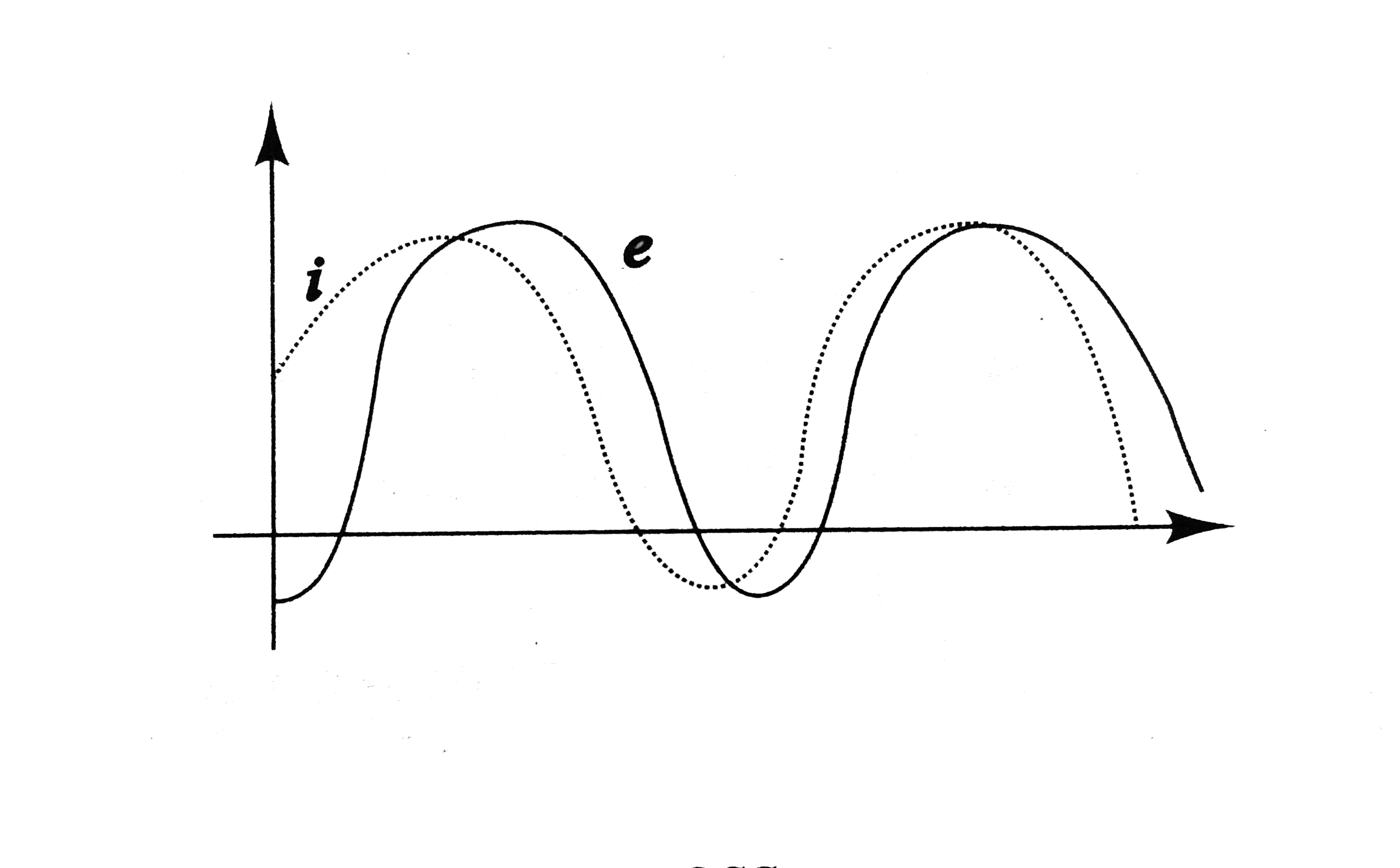
When an ac source of emf e=E_(0)sin(100t) is connected across a circuit,the phase difference between emf e and current i in the circuit is observed to be pi/4 as shown in figure.If the circuit consists possibly only of R-C or R-C or L-R series,find the relationship between the two elements.
View SolutionA pure inductance is connected to an AC source. What will be the phase difference between the current and the EMF in the circuit?
View Solution
Knowledge Check
When an ac source of emfe=E0sin(100t) is connected across a circuit, the phase difference between emf e and currnet I in the circuit is observed to be (π)/(4) as shown in fig. If the circuit consists possibly only of R-C or R-C of L-R series, find the relationship find the relationship between the two elements.
 AR=1kΩ,C=10(μ)FBR=1kΩ,C=1(μ)FCR=1kΩ,L=10(μ)FDR=1kΩ,L=1(μ)F
AR=1kΩ,C=10(μ)FBR=1kΩ,C=1(μ)FCR=1kΩ,L=10(μ)FDR=1kΩ,L=1(μ)FThe phase difference between voltage and current in series L-C circuit is
A0∘BπCπ2Dπ3An L-C-R circuit is connected to a source of A.C. current. At resonance, the phase difference between the applied voltage and the current in the circuit, is
AπBZeroCπ4Dπ2
An alternating e.m.f. 100 cos 100 t volt is connected in series to a resistance of 10 ohm and inductance 100mH. The phase difference between the current in the circuit and the e.m.f. is
View SolutionAn alternating e.m.f. 100 cos 100 t volt is connected in series to a resistance of 10 ohm and inductance 100mH. The phase difference between the current in the circuit and the e.m.f. is
View SolutionThe phase angle between e.m.f. and current in LCR series ac circuit is
View SolutionIf E0 is the peak emf , l0 is the peak current and ϕ is the phase difference between them, then the average power dissipation in the circuit is
View SolutionIn series LCR circuit, the phase angle between supply voltage and current is
View Solution
