An alternating current generator has an internal resistance Rg and an internal reactance Xg. It is used to supply power to a passive load consisting of a resistance Rg and a rectance XL. For maximum power to be delivered from the generator to the load, the value of XL is equal to
Zero
Xg
−Xg
Rg
The correct Answer is:C
For delivering maximum power from the generator to the load, total internal reactance must be equal to conjugate of total external reactance.
Hence , Xint=X∗ext
⇒Xg=(XL)∗=−XL⇒XL=−Xg
Similar Questions
An AC generator of 220 V having internal resistance r=10Ω and external resistance R=100Ω. What is the power developed in the external circuit?
View Solution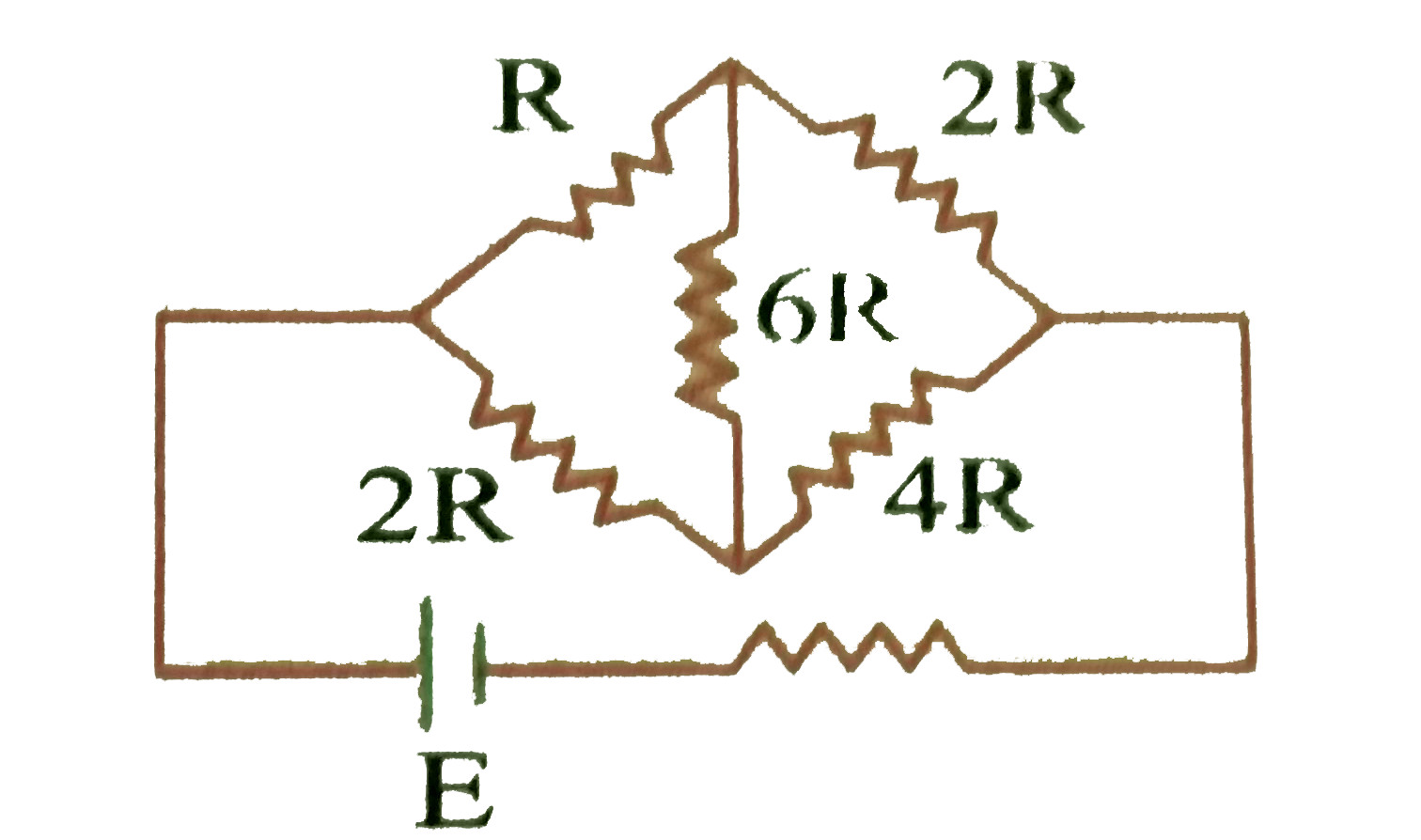
A battery if internal resistance 4Ω is conneted to the network of resistances as shown. What must be the value of R so that maximum power is delivered to the network Find the maximum power?
View Solution
Knowledge Check
An AC generator of 220 V having internal resistance r=10Ω and external resistance R=100Ω. What is the power developed in the external circuit?
A484 WB400 WC441 WD369 WA battery of internal resistance 4Ω is connected to the network of resistance as shown . In order that the maximum power can be delivered to the network, the value of R in Ω should be
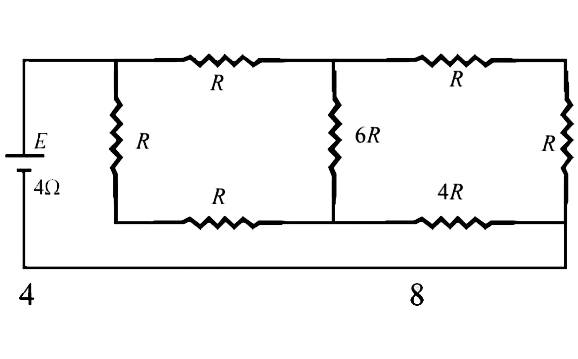 . A49B2C83D18
. A49B2C83D18A battery of internal resistance 4Ω is connected to the network of resistance as shown . In order that the maximum power can be delivered to the network, the value of R in Ω should be
 . A49B2C83D18
. A49B2C83D18
A cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
(ii) Draw the power (P ) vs load resistance ( R ) graph.
View SolutionA parallel combination of two cells of emfs ε1 and ε2, and internal resistance r1 and r2 is used to supply current to a load of resistance R. Write the expression for the current through the load in terms of ε1,ε2,r1 and r2.
View SolutionFor maximum power from battery the internal resistance of battery r is
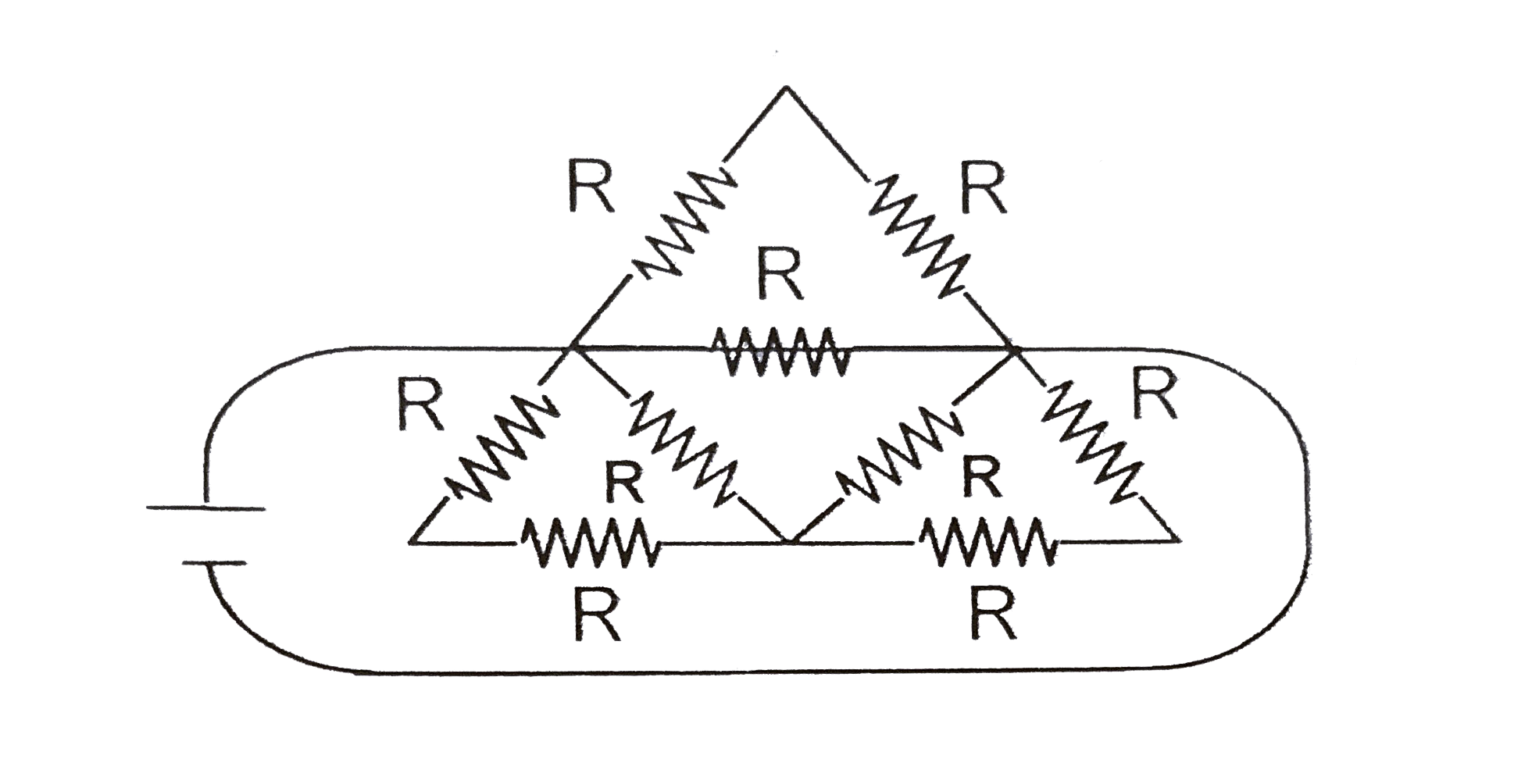
View SolutionA battery is of emt E and internal resistance r. The value of external resistance R so that the power across eternal resistance is maximum :
View SolutionCell A has emf 2 E ad internal resistance 4 r. Cell B has emf E and internal resistance r. The negative of A is connected to the positive of B and a load resistance of R is connected across the battery formed. If the terminal potential difference across A is zero, then R is equal to
View Solution
