A highly conucting ring of radius R is perpendicular to and concentric with the axis of a long solenoid as shown in fig. the ring has a narrow gap of width d in its circumference. The solenoid has cross sectional area A and a uniform internal field of magnitude B0. Now beginning at t=0, the solenoid current is steadily increased to so that the field magnitude at any time t is given by B(t)=B0+αt where α>0. Assuming that no charge can flow across the gap, the end of ring which has excess of positive charge and the magnitude of induced e.m.f. in the ring are respectively

X, Aα
X, πR2α
Y, πA2α
Y, πR2α
The correct Answer is:A
e=ddt(BA)=Addt(B0+αt)=Aα
X → excess +ve charge because current flows in wing from Y to X (by Len.z law).
Similar Questions
A long wire carries a current of 20A along the directed axis of a long solenoid. The field due to a solenoid is 4mT. Find the resultant field at a point 3mm from the solenoid axis.
View SolutionA solenoid consists of 250 turns of wire and has a length of 20 cm. Calculate the magnitude of the magnetic field inside the solenoid if it carries a current of 1A.
View Solution
Knowledge Check
A highly conducting ring of radius R is perpendicular to and concentric with the axis of a long solenoid as shown in Fig. 3.182. The ring has a narrow gap of width δ in its circumference. The cross-sectional area of the solenoid is a. The solenoid has a unifoem unitial field of magnitude B(t)=B0+βt, where β>0. Assuming that no charge can flow across the gap, the face (s) accumulating an excess of positive charge is /are
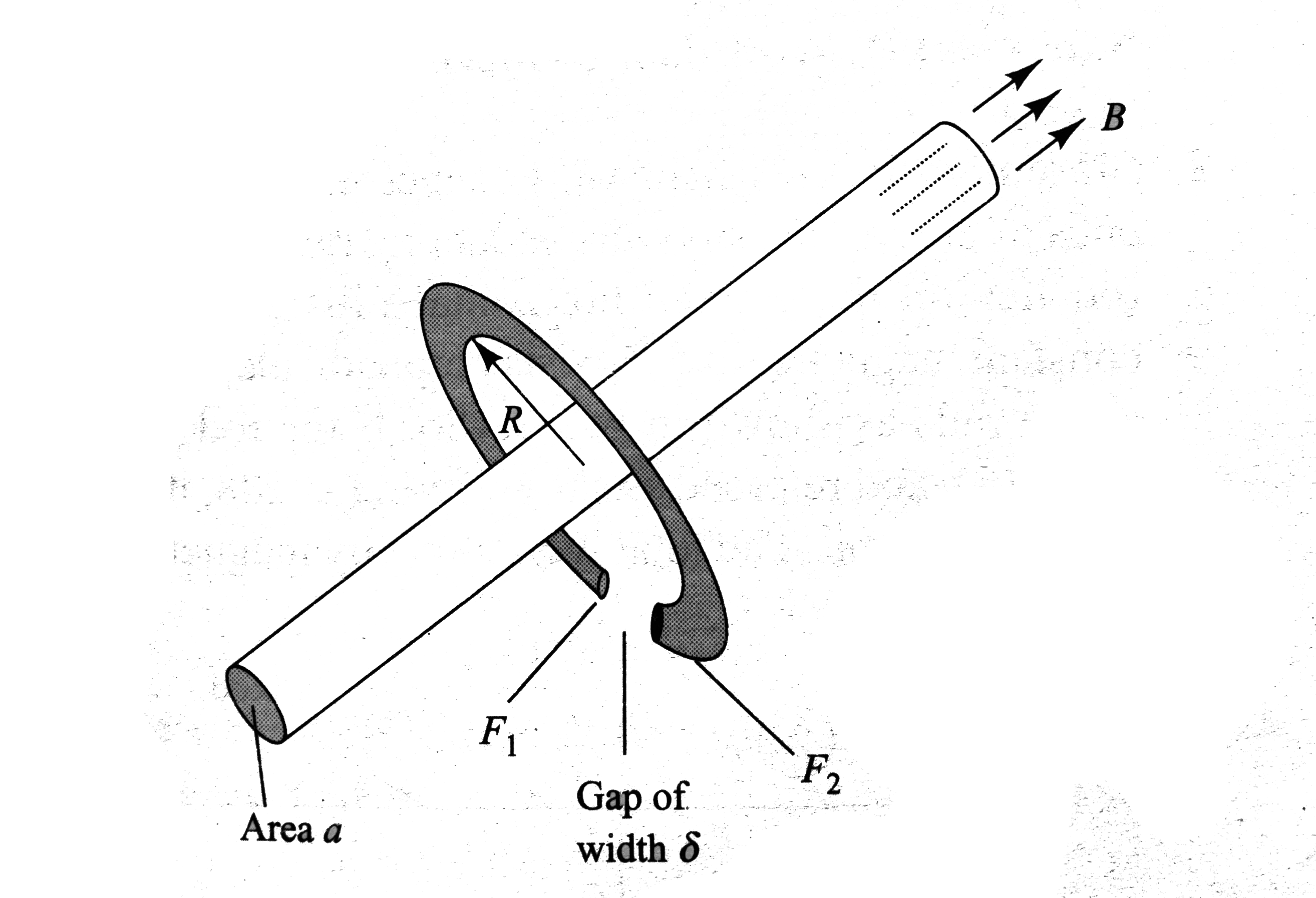 A(a) F1B(b) F2C( c) F1andF2 bothD(d) difficult to conclude as data given are insufficient
A(a) F1B(b) F2C( c) F1andF2 bothD(d) difficult to conclude as data given are insufficientThe ring B is coaxial with a solenoid A as shown in figure. As the switch S is closed at t=0, the ring B
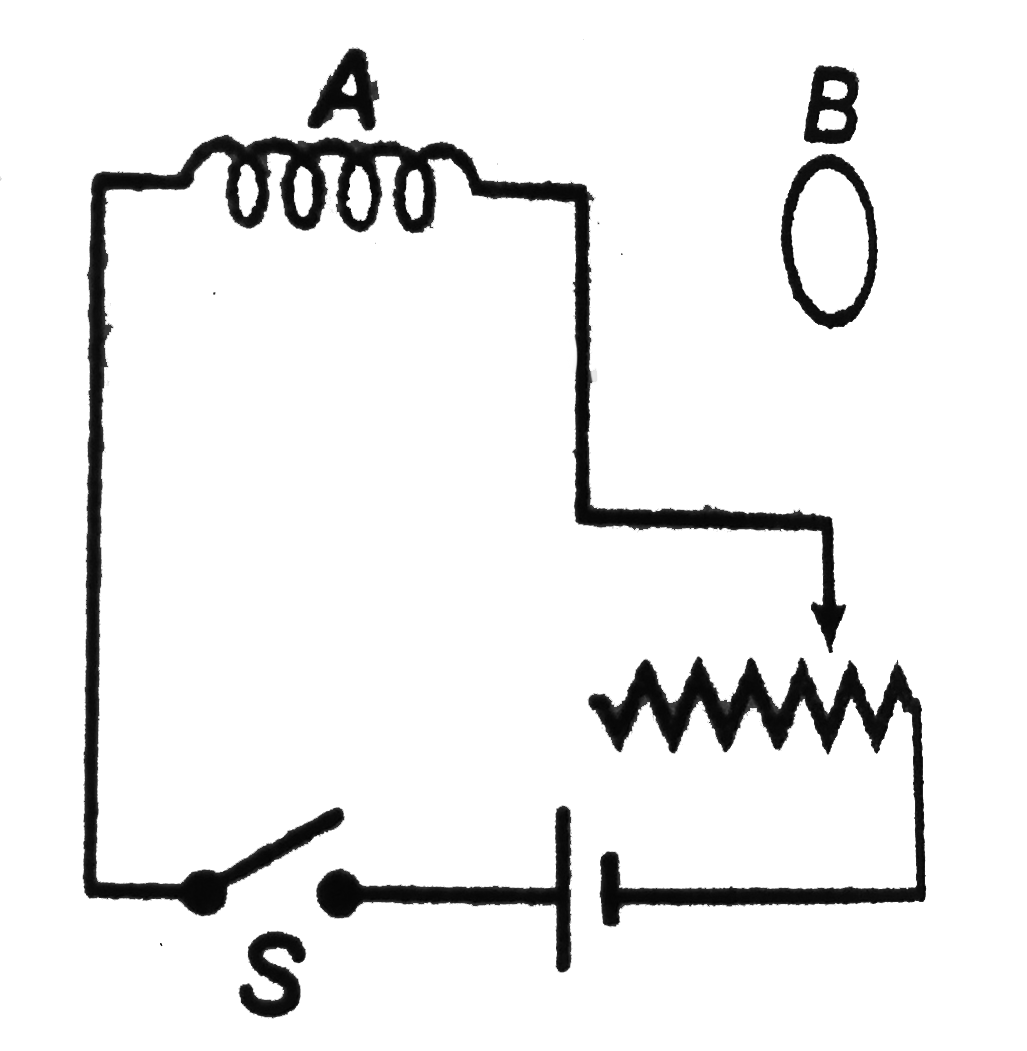 Ais attracted towards ASBis repelled by ACis initially repelled and then attractedDis initially attracted and then repelled
Ais attracted towards ASBis repelled by ACis initially repelled and then attractedDis initially attracted and then repelledThe magnitude of the magnetic field inside a long solenoid is increased by
Adecreasing its radiusBdecreasing the current throught itCincreasing its area of cross sectionDintroducing a medium of higher permeability
A 0.8 m long solenoid has 800 turns and a field density of 2.52×10−3 T at its certre .Find the current in the solenoid
View SolutionA long solenoid has n turns per metre and current IA is flowing through it. The magnetic field induciton at the ends of the solenoid is
View SolutionA direct current flows in a solenoid of length L and radius R,(K>>R) , producing a magnetic field of magnetic B0 inside the solenoid
 .
.
View SolutionA horizontal ring of radius r spins about its axis with an angular velocity ω in a uniform vertical magnetic field of magnitude B. The emf induced in the ring is
View SolutionA ring of area A and resistance R is placed on the axis of a solenoid. The mutual inductance between them is M. When the current in the solenoid changes at the rate of I, the magnetic moment of the ring is
View Solution
