Two identical wires AandB , each of length 'l', carry the same current I. Wire A is bent into a circle of radius RandwireB is bent to form a square of side 'a' . If BAandBB are the values of magnetic field at the centres of the circle and square respectively , then the ratio BABB is :
π216√2
π216
π28√2
π28
The correct Answer is:C
Magnetic field at centre -
BA=μ0I2R
∴2πr=l⇒R=l2π
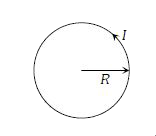
BA=μ0Iπl ..(i)
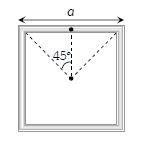
Magnetic field at centre –
BB=16μ0I√2πl
BABB=μ0Iπl×√2πl16μ0I
=√2π216=π28√2
Similar Questions
Two wires A and B have the same length equal to 44cm. and carry a current of 10A each. Wire A is bent into a circle and wire B is bent into a square. (a) Obtain the magnitudes of the fields at the centres of the two wires. (b) Which wire produces a greater magnetic field at the centre?
View SolutionA wire is bent to form a square of side 22 cm. If the wire is rebent to form a circle, its radius is
View Solution
Knowledge Check
Two identical wires A and B have the same length l and carry the same current I. Wire A is bent into a circle of radius R and wire B is bent to form a square of side a. If B1andB2 are the values of magnetic induction at the centre of the circle and the centre of the square, respectively, then the ratio B1/B2 is
A(π2/8)B(π2/8√2)C(π2/16)D(π2/16√2)Two identical wires A and B have the same length L and carry the same current I. Wire A is bent into a circle of radius R and wire B is bent to form a square of side a. If B1andB2 are the values of magnetic induction at the centre of the square respectively, then the ratio is B1B2 is
A(π28)B(π28√2)C(π216)D(π216√2)A wire of length l, carrying current i, is bent in circle of radius r, then magnetic momennt at centre of loop is
Al2i2πBl2i4πCli22πDli4π
A wire is in the form of a circle of radius 21cm. If is bent into a square, then side of the square is
View SolutionA wire of length L metre carrying a current of I ampere is bent in the form of a circle. Find its magnetic moment.
View SolutionA wire is bent in the form of a square of side 66 m . It is cut and again bent in the form of a circle. The diameter of this circle is :
View SolutionA wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is
View SolutionA wire of length L carrying a current I is bent into a circle. The magnitude of the magneitc field at the centre of the circle is
View Solution
