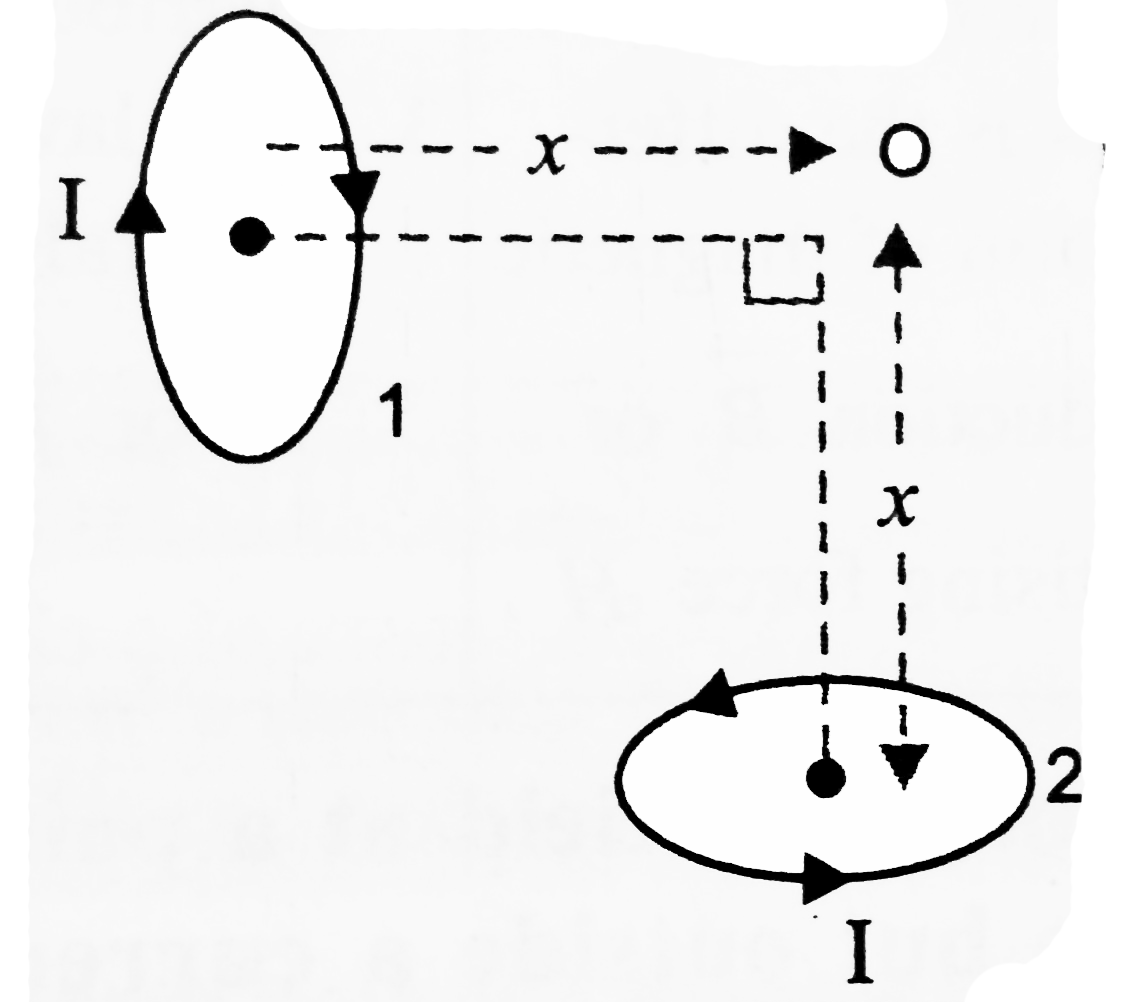
Two coaxial circular loops and of radii and are placed as shown in figure. What should be the magnitude and direction of the current in the loop so that the net magnetic field at the point O be zero?

The correct Answer is:
The resultant magnetic field at the point will be zero only if the direction of current in loop is opposite to that in loop
Then magnetic field at O due to current in loop = magnetic field at O due to current in loop
or
or
or
or
Similar Questions
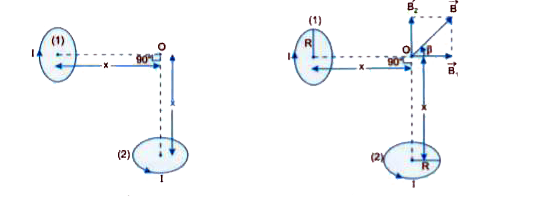
Two small identical circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in the fig. Find the fig. Find the magnitude and direction of the net magnetic field at the net magnetic field at the point O.
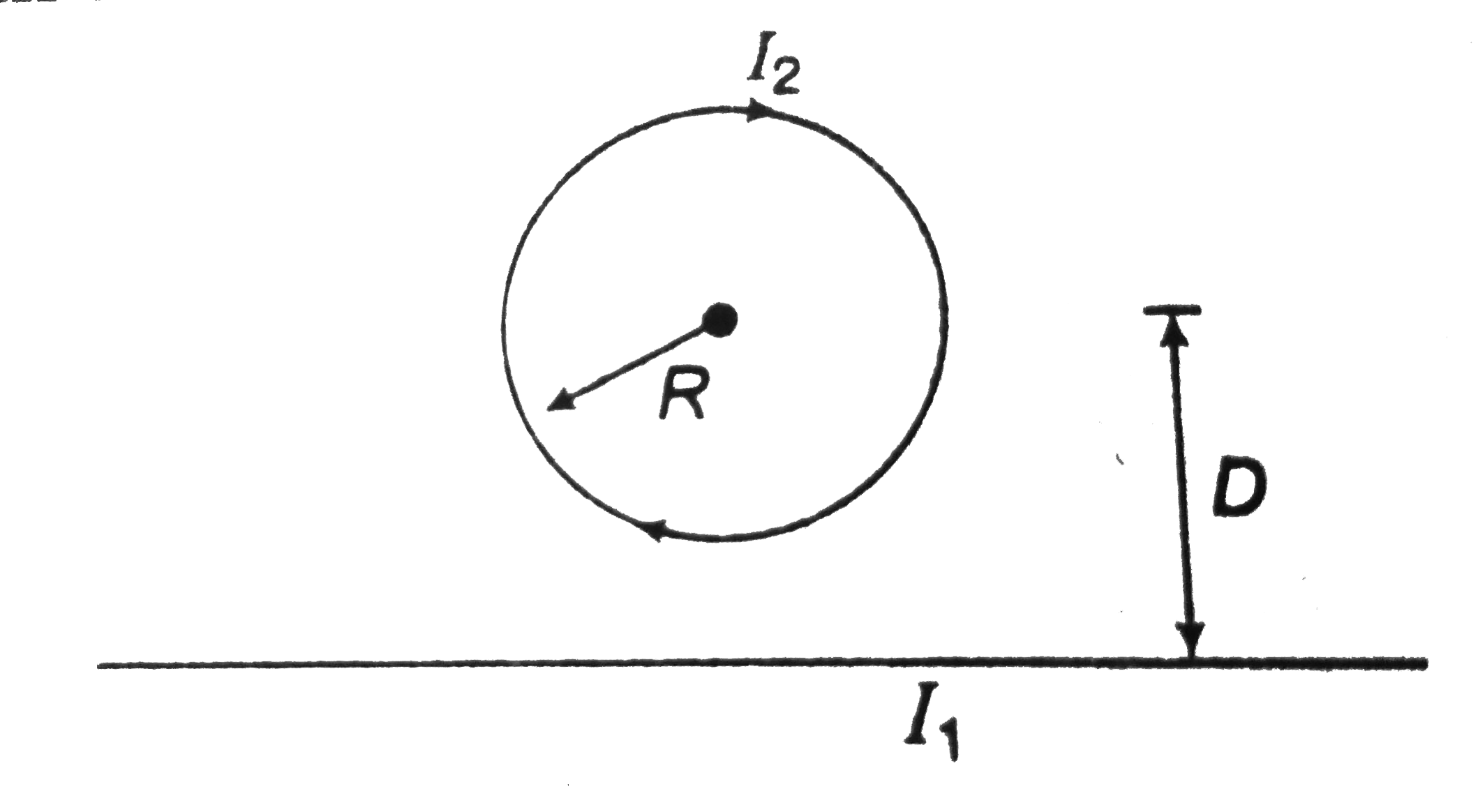
View SolutionA circular loop of radius R carries current I2 in a clockwise direction as shown in figure. The centre of the loop is a distance D above a long, straight wire. What are the magnitude and direction of the current I1 in the wire if the magnetic field at the centre of loop is zero?
View Solution
Knowledge Check
A triangular loop is placed in a dot ⊙ magnetic field as shown in figure. Find the direction of induced current in the loop if magnetic field is increasing.
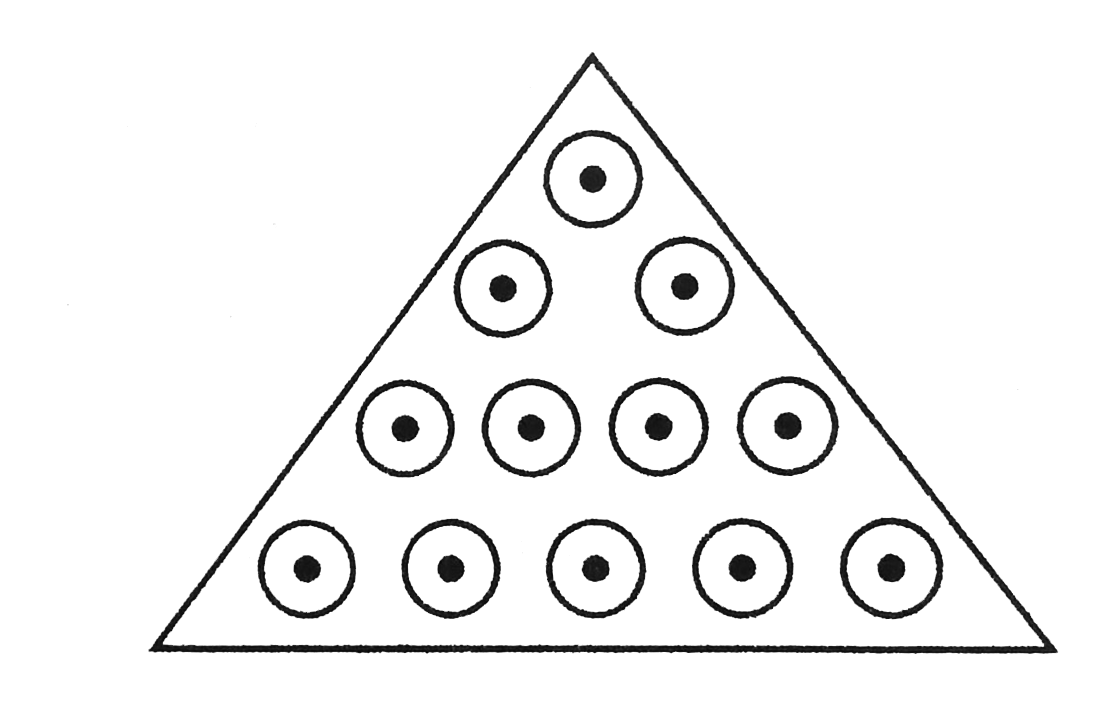 AAnti-clockwiseBrandomCClockwiseDno induced current
AAnti-clockwiseBrandomCClockwiseDno induced currentA current I flows through a closed loop as shown in figure .The magnetic field at the centre O is
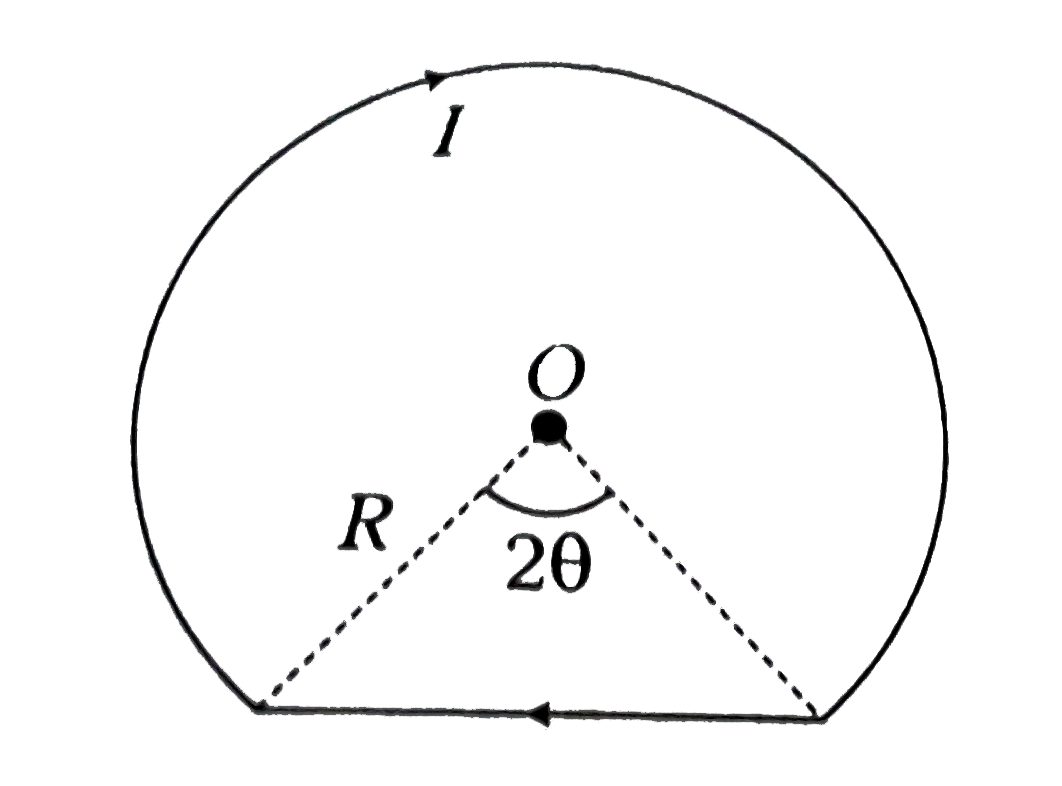 Aμ0I2πR(π−θ+tanθ)Bμ0I2πR(π−θ+sinθ)Cμ0I2πR(θ+sinθ)DNone of these
Aμ0I2πR(π−θ+tanθ)Bμ0I2πR(π−θ+sinθ)Cμ0I2πR(θ+sinθ)DNone of theseA circular loop is placed in magnetic field B=2t. Find the direction of induced current produced in the loop.
 AClockwiseBAnti clockwiseCNo induced currentDrandom direction
AClockwiseBAnti clockwiseCNo induced currentDrandom direction
Two circular loops of radius 6 cm and 8 cm are kept in Y-Z plane with their centres at (0, 0, 0) and (14 cm, 0, 0). Current in the first loop is 1 A and is in an anticlockwise direction, when seen from the second loop. Calculate the magnitude and direction of current in the second loop such that net magnetic field at point (8 cm, 0, 0) is zero.
View SolutionA circular loop has radius R and carries current I2 in a clockwise direction (as shown in Fig.) The centre of the loop is at a distance D above a long, straight wire. What are the magnitude and direction of the current I1 in the wire if the magnetic field at the center of the loop is zero?

View SolutionTwo small circular loops, marked (1) and (2), carrying equal currents are placed with the geometrical axes perpendicular to each other as shown in figure. Find the magnitude and direction of the net magnetic field produced at the point O.
View SolutionA square loop of side l carries a current i. it is placed as shown in figure. Find the magnetic moment of the loop.
View SolutionA non - planar loop of conducting wire carrying a current I is placed as shown in the figure . Each of the straighrt sections of the loop is of the length 2a. The magnetic field due to this loop at the point P(a,0,a) points in the direction

View Solution
