Seven identical coins are rigidly arranged on a flat table in the pattern shown below so that each coin touches its neighbors. Each coin is a thin disc of mass m and radius r. Note that the moment of inertia of an individual coin about an axis passing through centre and perpendicular to the plane of the coin is m2/2
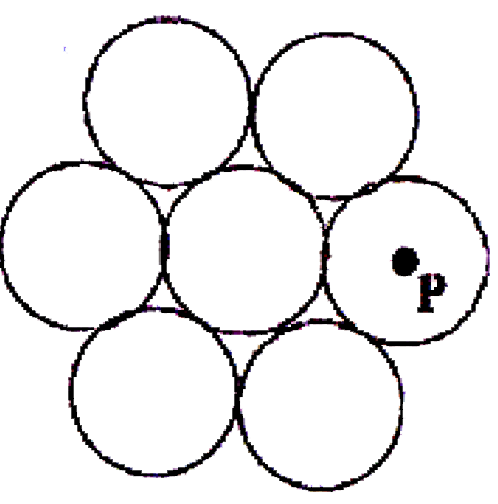
The moment of inertia of the system of seven coins about an axis that passes through the point P (the centre of the coin positioned directly to the right of the central coin) and perpendicular to the plane of the coins is–
552mr2
1272mr2
1112mr2
55mr2
The correct Answer is:C
Ip=mr22+3[mr22+m(2r)2]+[mr22+m(r2√3)2]×2+[mr22+(4r)2m]
=1112mr2

Similar Questions
The moment of Inertia of a uniform semicircular disc of mass M and radius 'r' about a line perpendicular to the plane of the disc through the centre is :
View SolutionThe moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the centre is ………..
View SolutionA coin of mass m and radius r having moment of inertia I about the axis passing through its centre and perpendicular to its plane. It is beaten uniformly to form a disc of radius 2r. What will be the moment of inertia about the same axis?
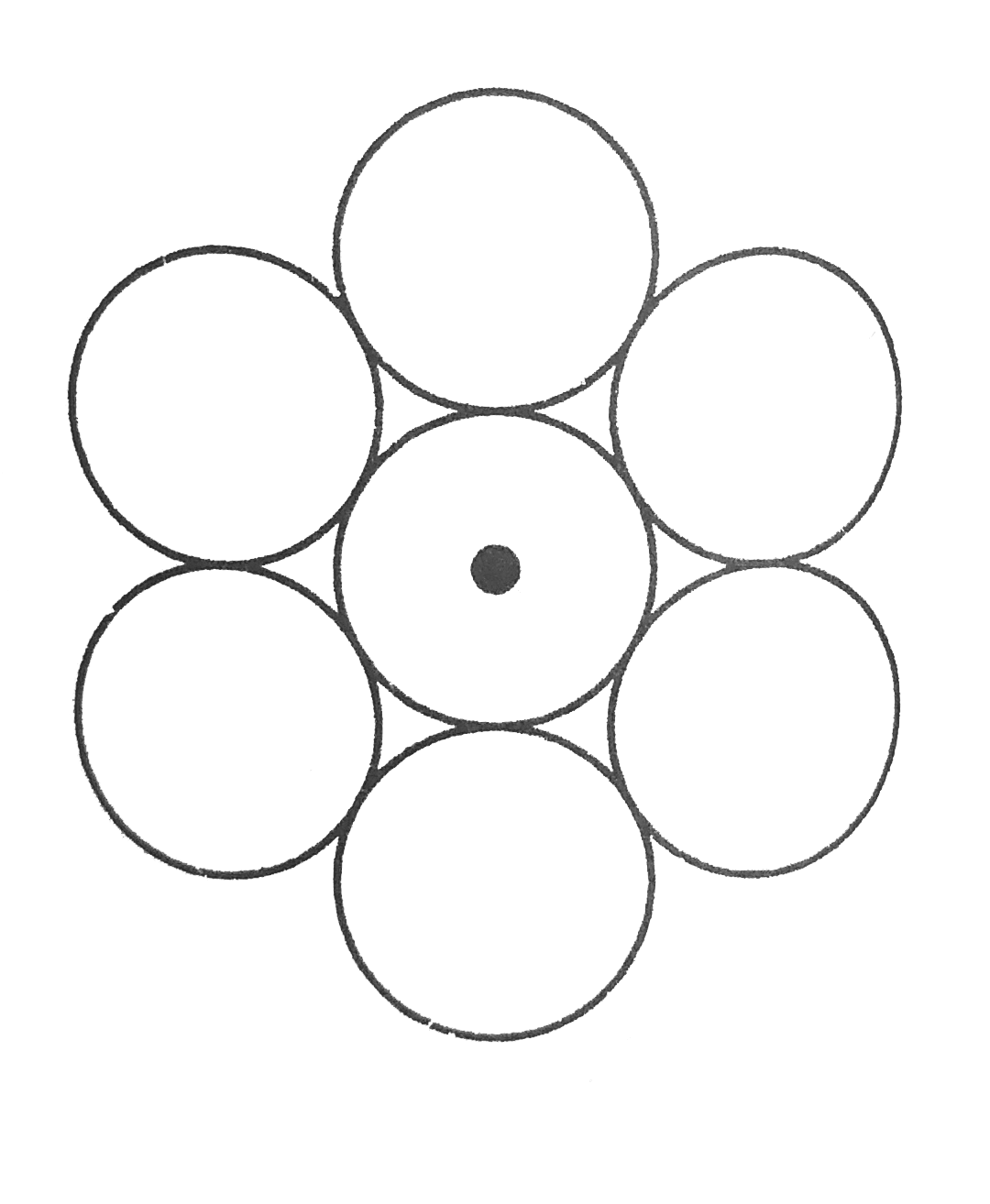
View SolutionSeven identical disc are arranged in a hexagonal, planar pattern so as to touch each neighbour, as shown in the figure. Each disc has mass m and radius r. What is the moment of inertia of the system of seven disks about an axis passing through the centre of central disk and normal to plane of all disks ?
 .
.
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionState an expression for moment inertia of a thin uniform disc about an axis passing through its centre and perpendicular to its plane .
View SolutionThe moment of inertia of a disc about an axis passing through its centre and perpendicular to its plane is 20 kg m^2 . Determine its moment of inertia about an axis coinciding with a tangent perpendicular to its plane
View SolutionThe moment of inertia of a disc about an axis passing through its centre and perpendicular to its plane is 0.4 kg m^2 . Calculate its moment of inertia about tangent perpendicular to the plane of the disc.
View Solution
