A smaller cube with side b (depicted by dashed lines) is excised from a bigger uniform cube with side a as shown below such that both cubes have a common vertex P. Let X = a/b. If the centre of mass of the remaining solid is at the vertex O of smaller cube then X satisfies.

x3−x2−x−1=0
x2−x−1=0
x3+x2−x−1=0
x3−x2−x+1=0
The correct Answer is:A
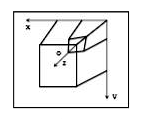
XCM=ρ(a3)(a2)−ρ(b3)(b2)ρ(a3)−ρ(b3)
We will consider removed mass as a negative mass
b=ρ(a42)−ρ(b42)ρ(a3)−ρ(b3)
a3b−b4=a42−b42
2a3b−2b4=a4−b4
Put a= bx,
2b4x3−2b4=b4x4−b4
2x3−1=x4
2x3−2+1=x4
2(x3−1)=(x2+1)(x2−1)
2(x−1)(x2+1+x)=(x−1)(x+1)(x2+1)
2x2+2+2x=x3+x+x2+1
x3−x2−x−1=0
Similar Questions
b भुजा वाले एक घन के प्रत्येक शीर्ष q आवेश है। इस आवेश विन्यास के कारण घन के केंद्र पर विद्युत विभव होगा।
View SolutionA solid cube with an edge 10 cm is melted to form two equal cubes. The ratio of the edge of the smaller cube to the edge of the bigger cube is
View SolutionThe volume of two cubes are in the ratio 1 : 64. If the volume of the larger cube is 504 cm3 more than that of the smaller cube, then
(i) What is the volume of the smaller cube?
(ii) What is the length of each side of the larger cube?
View Solution128 parts to a cube. has been divided into. The side of the smaller cubes obtained by this division is 3 cm. What would have been the side of the bigger cube?
View SolutionThe side of a cube is 2 cm. It is divided into smaller cubes of side 0.5 cm. How many cubes will be obtained in this way?
View SolutionHow many smaller cubes of 1 cm side can be formed with a solid cube of 3 cm side ?
View SolutionA cube of 3 cm side is divided into smaller cubes of side 1 cm. What will be the total number of middle cubes?
View SolutionIf a cube of 12 cm side is divided into smaller cubes of 3 cm side, then find the total number of inner central cubes?
View Solution
