Two condensers, one of capacity C and the other of capacity , are connected to a V-volt battery, , as shown

The work done in charging fully both the condensers is
The correct Answer is:C
Similar Questions
A condenser of capacity 16 mF charged to a potential of 20 V is connected to a condenser of capacity C charged to a potential of 10 V as shown in the figure.

If the common potential is 14 V. the capacity C is equal to
View SolutionTwo condensers, one of capacity C and the other of capacity C/2 are connected to a V volt battery, as shown.
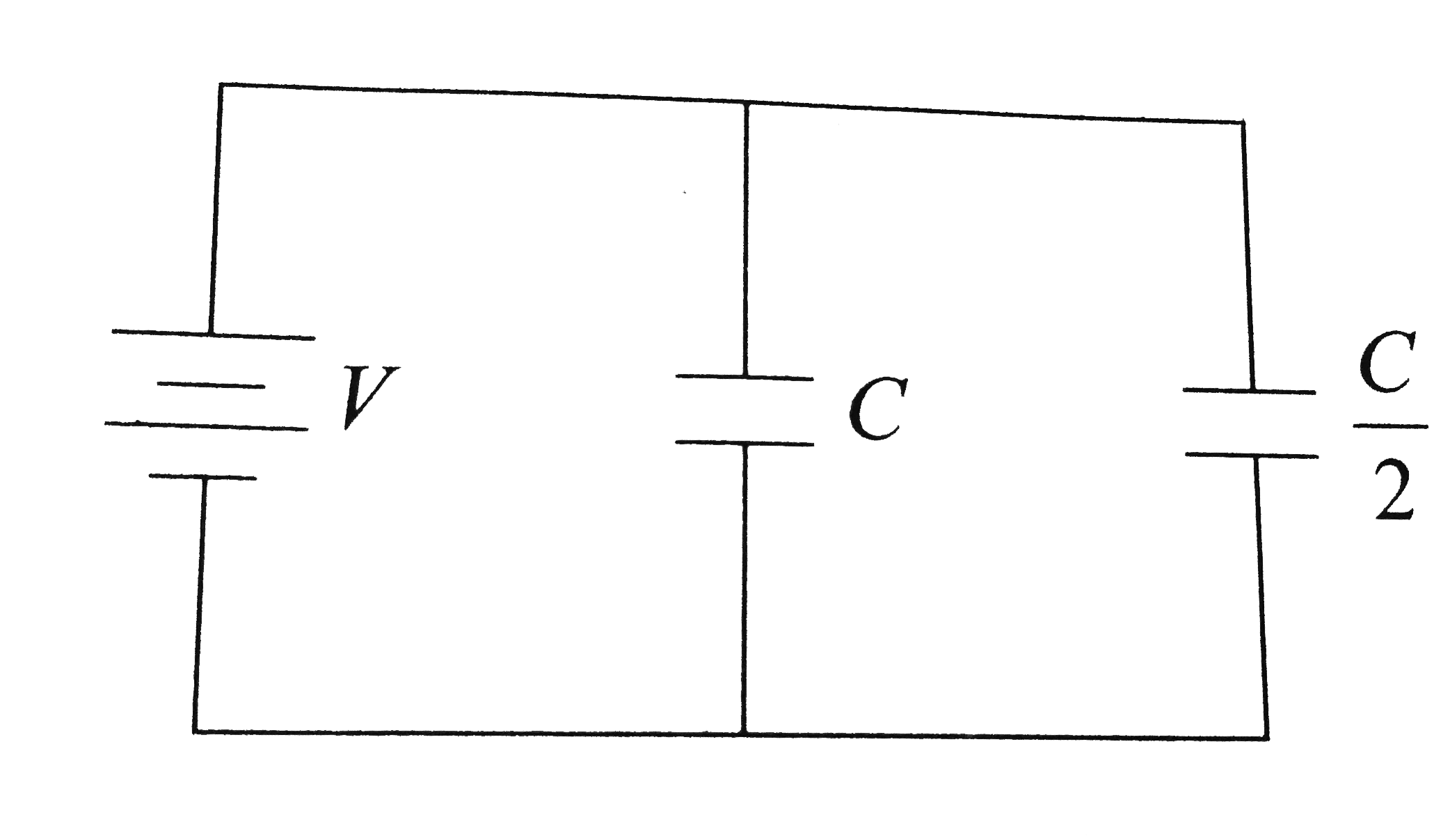
The work done in charging fully both the condensers is
View SolutionTwo condensers of capacities C and 3C are connected in parallel and then connected in series with a third condenser of capacity 3C. The combination is charged with a battery of 'V'volt. The charge on condenser of capacity C is (in coulomb)
View SolutionTwo condensers, one of capacity C and the other of capacity C/2 are connected to a V volt battery, as shown.

The work done in charging fully both the condensers is
View SolutionTwo condensers, one of capacity C and the other of capacity C/2 are connected to a V volt battery, as shown.

The work done in charging fully both the condensers is
View SolutionTwo condensers, one of capacity C and the other of capacity C/2 are connected to a V volt battery, as shown.

The work done in charging fully both the condensers is
View SolutionTwo condensers, one of capacity C and the other of capacity C/2 are connected to a V volt battery, as shown.

The work done in charging fully both the condensers is
View SolutionTwo condensers, one of capacity C and the other of capacity C2, are connected to a V volt battery, as shown in figure.
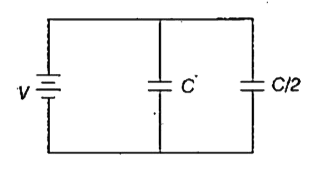
The work done in charging fully both the condensers is
View Solution
