At a given temperature, the pressure of an ideal gas of density is proportional to
The correct Answer is:D
Since, speed of sound .
Similar Questions
During an experiment, an ideal gas is found to obey a condition P2ρ constant [ρ = density of the gas]. The gas is initially at temperature. T, pressure P and density ρ . The gas expands such that density changes to ρ2
View SolutionIf the pressure, temperature and density of an ideal gas are denoted by P, T and ρ, respectively, the velocity of sound in the gas is
View SolutionThe density of the given gas at constant pressure and temperature is rho and its rate of diffusion isr. If density of the gas becone rho//3 then rate of diffusion becomes
View SolutionIf the pressure, temperature and density of an ideal gas are denoted by P.T and rho respectively. The velocity of sound in the gas is
View SolutionDuring an experiment, an ideal gas is found to obey a condition (p^2)/(rho) = "constant" . ( rho = density of the gas). The gas is initially at temperature (T), pressure (p) and density rho . The gas expands such that density changes to rho//2 .
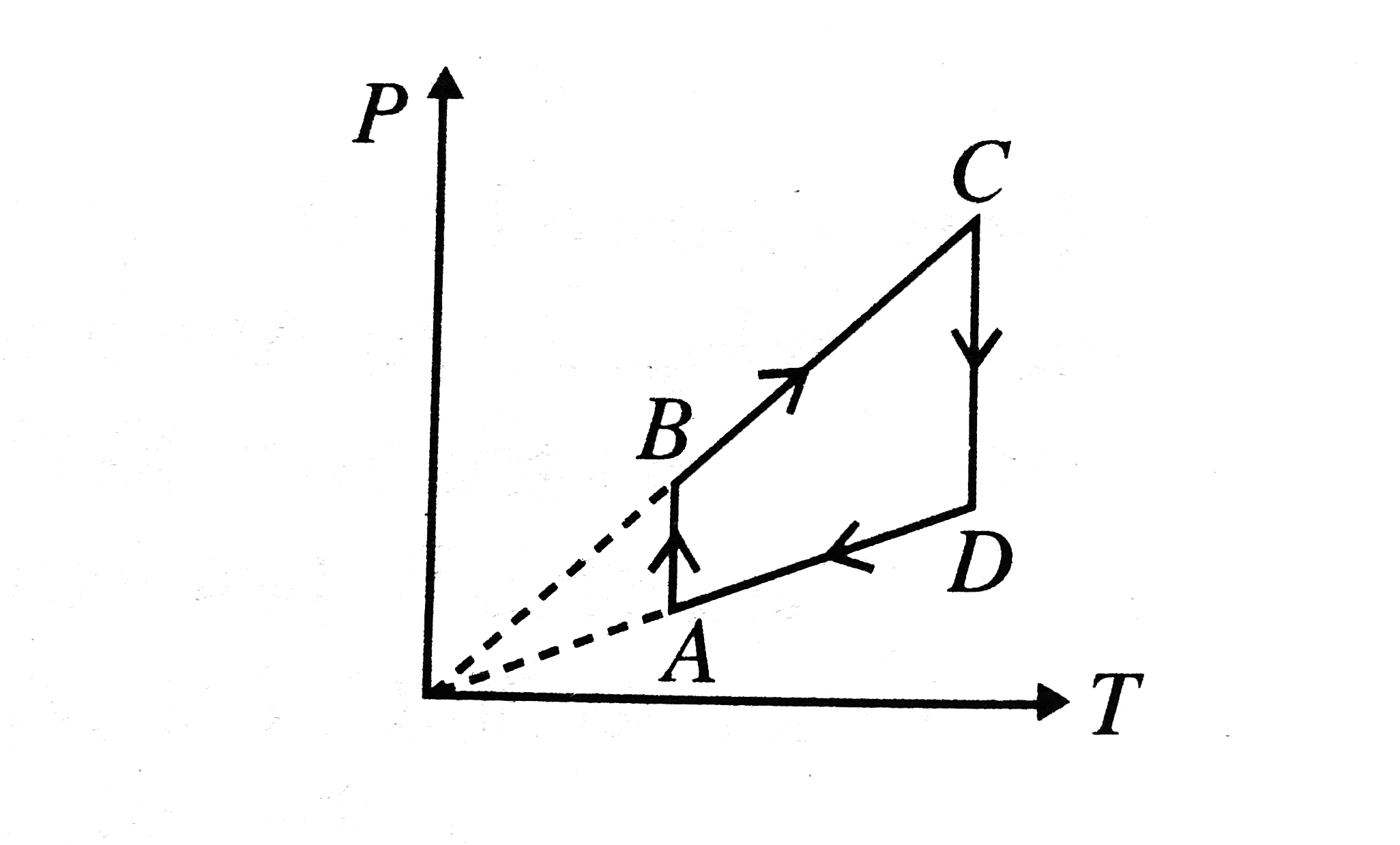
View SolutionPressure versus temperature graph of an ideal gas as shown in Fig.
Corresponding density (ρ) versus volume (V) graph will be
View SolutionThe density of the given gas at constant pressure and temperature is rho and its rate of diffusion isr. If density of the gas becone rho//3 then rate of diffusion becomes
View SolutionPressure versus temperature graph of an ideal gas as shown in Fig.
Corresponding density (ρ) versus volume (V) graph will be

View Solution
