A simple pendulum of length l and mass (bob) m is suspended vertically. The string makes an angle θ with the vertical. The restoring force acting on the pendulum is
mv2/L
mg.cosθ+mv2/L
mg.cosθ−mv2/L
mg.cosθ
The correct Answer is:B
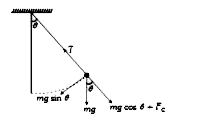
From the figure T=mgcosθ+mv2/L
Similar Questions
A simple pendulum of length 'l' has a bob of mass 'm'. If it is released when the string makes an angle 60^(@) with the vertical, the tension in the string at the lowest position is
View SolutionA simple pendulum of length 'l' has a bob of mass 'm'. If it is released when the string makes an angle 60^(@) with the vertical, the tension in the string at the lowest position is
View SolutionA simple pendulum of length L swings in a vertical plane. The tension of the string when it makes an angle θ with the vertical and the bob of mass m moves with a speed v is (g is the gravitational acceleration)
View SolutionA simple pendulum of length L swings in a vertical plane. The tension of the string when it makes an angle θ with the vertical and the bob of mass m moves with a speed v is (g is the gravitational acceleration)
View SolutionA simple pendulum of length I and mass (bob) m is suspended vertically. The string makes an angle theta with the vertical. The restoring force acting on the pendulum is
View SolutionA simple pendulum of length I and mass (bob) m is suspended vertically. The string makes an angle θ with the vertical. The restoring force acting on the pendulum is
View SolutionWhat is the torque acting on the bob of mass m of a simple pendulum Of length l, when the string of the pendulum makes an angle θ with the vertical ? When is the torque (i) zero and (ii) maximum.
View SolutionA simple pendulum of length l swings in a vertical plane. The tension of the string when it makes an angle theta with the vertical and the bob of mass m moves with a speed v is (g is the gravitational acceleration)
View Solution
