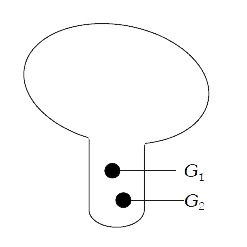
G1 and G2 are genetically identical because

They are products of meiosis I
They are products of amitosis
They are products of meiosis
They are products of mitosis
The correct Answer is:D
They are product of mitosis in which generative cell divides mitotically to form two male gametes both are non motile. The male gamete enters in the ovary at the time when ovule becomes mature.
Similar Questions
If G1 and G2 are two geometric means and A is the arithmetic mean inserted two numbers, then the value of G21G2+G22G1 is:
View SolutionIf G1andG2 are two geometric means and A the asrithmetic mean inserted between two numbers, then the value of G21G2+G22G1 is (A) A2 (B) A (C) 2A (D) none of these
View Solution
Knowledge Check
G1 and G2 genetically identical because
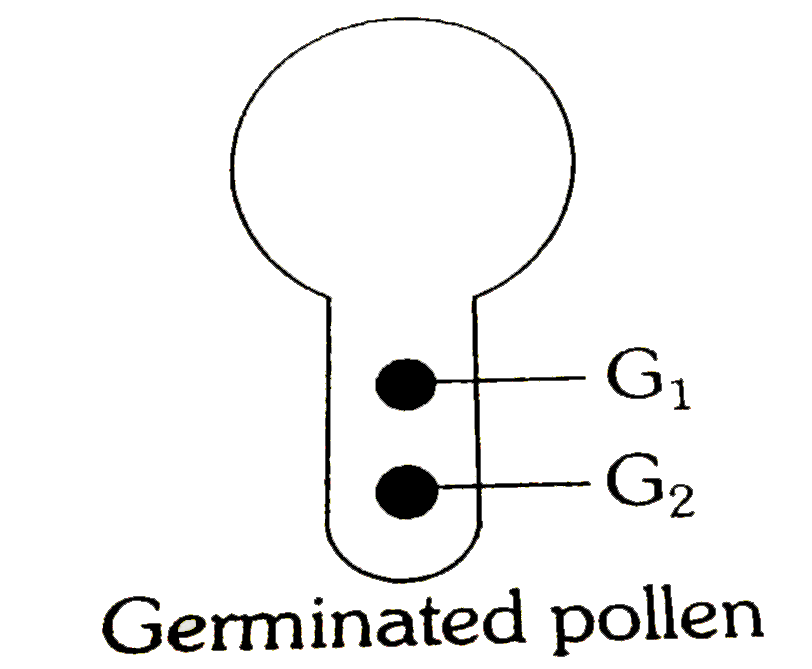 AThey are products of meiosis IBThey are products of amitosisCThey are products of meiosisDThey are products of mitosis
AThey are products of meiosis IBThey are products of amitosisCThey are products of meiosisDThey are products of mitosisG1,SandG2 are stages of
AinterphaseBprophaseCmetaphaseDanaphaseAsexual reproduction produces genetically identical individuals because-
AChromosome do not have to replicateBIt involves chromosome replication without cytokinesisCNo meiosis or fertilization takes placeDThe only cell division that occurs in meiosis.
⎡⎣H2(g)+12O2(g)=H2O(g)ΔH=−241.8kJC2H2(g)+212O2(g)=2CO2(g)+H2O(g)ΔH=−1300kJ⎤⎦
Equal volumes of C2H2 and H2 are combusted under identical conditions. The ratio of heats evolved in the two cases is
View SolutionEqual volumes of C2H2 and H2 are combusted under identical conditons. The ratio of evolved in i.e. for C2H2 and H2 is:
H2(g)+12O2(g)→H2O(g),ΔH=−241.8 kJ
C2H2(g)+212O2(g)→2CO2(g)+H2O(g),ΔH=−1300 kJ
View SolutionEqual volume of C2H2 and H2 are combusted under identical condition , The ratio of their enthalpy of comabution is
H2(g)+(1/2)O2(g)=H2O(g),ΔH=−241.8KJ
C2H2(g)+(5/2)O2(g)=2CO2(g)+H2O(g)ΔH=−1300KJ
View SolutionAssertion: DNA synthesis occurs in G1 and G2 periods of cell cycle.
Reason: During G1 and G2 phase the DNA contents become double.
View SolutionThe formation of water from H2(g) and O2(g) is an exothermic process because :
View Solution
