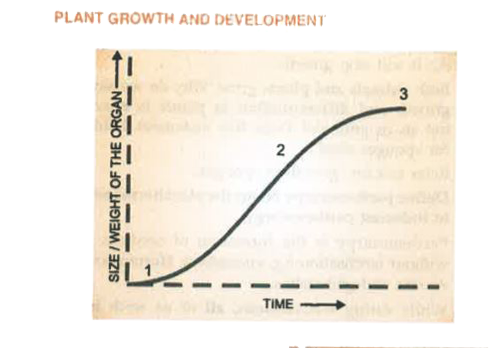
Sigmoid growth curve define by
Malthus
Adam Smith
Verhulst
Charles Darwin
The correct Answer is:C
Step-by-Step Solution:
1. Understanding the Sigmoid Growth Curve:
- The sigmoid growth curve is a graphical representation of population growth that shows how a population increases rapidly at first, then slows down as it approaches a certain limit, resulting in an S-shaped curve.
2. Defining the Sigmoid Growth Curve:
- The sigmoid growth curve is defined by logistic growth, which describes how populations grow in an environment with limited resources.
3. Key Contributors:
- The sigmoid growth curve was defined by several scientists, including Warholz and Perl. Their work contributed significantly to our understanding of logistic growth.
4. Logistic Growth Equation:
- The mathematical representation of logistic growth is given by the equation:
dndt=r⋅n⋅(k−nk)
- Where:
- n = population density at time t
- r = intrinsic rate of natural increase
- k = carrying capacity of the environment
5. Interpreting the Variables:
- dndt: This represents the change in population size over time.
- r: This is the rate at which the population grows when resources are unlimited.
- k: This is the maximum population size that the environment can sustain.
6. Conclusion:
- The sigmoid growth curve is fundamentally linked to logistic growth, and it is characterized by its S-shape due to the initial exponential growth followed by a slowdown as the population reaches its carrying capacity.
- The sigmoid growth curve is a graphical representation of population growth that shows how a population increases rapidly at first, then slows down as it approaches a certain limit, resulting in an S-shaped curve.
- The sigmoid growth curve is defined by logistic growth, which describes how populations grow in an environment with limited resources.
- The sigmoid growth curve was defined by several scientists, including Warholz and Perl. Their work contributed significantly to our understanding of logistic growth.
- The mathematical representation of logistic growth is given by the equation:
dndt=r⋅n⋅(k−nk)
- Where:
- n = population density at time t
- r = intrinsic rate of natural increase
- k = carrying capacity of the environment
- dndt: This represents the change in population size over time.
- r: This is the rate at which the population grows when resources are unlimited.
- k: This is the maximum population size that the environment can sustain.
- The sigmoid growth curve is fundamentally linked to logistic growth, and it is characterized by its S-shape due to the initial exponential growth followed by a slowdown as the population reaches its carrying capacity.
Similar Questions
Knowledge Check
Assertion: Sigmoid growth curve consists of four parts.
Reason : Lag phase is called as grand phase of growth.AIf both A and R are true and R is the correct explanation of ABIf both A and R are true but R is not the correct explanation of ACIf A is true and R is falseDIf both A and R are falseAssertion: Sigmoid growth curve consists of four parts.
Reason : Lag phase is called as grand phase of growth.AIf both the assertion and the reason are true and the reason is a correct explanation of the assertion.BIf both the assertion and reason are true but the reason is not a correct explanation of the assertionCIf the assertion is true but the reason is falseDIf the assertion and reason is false but reason is trueIf in a population showing sigmoid growth curve the value of K-N/K is 0.95 then what is true for this population.
AThe carrying capacity has been nearly realizedBThe carrying capacity has not been substantially realized and it can accmmodate many more organismsCThe carrying capacity is only 50% realizedDData is insufficient to comment anything
Growth curve is
View SolutionIn the figure of sigmoid growth cureve given below label segments 1,2 and3.
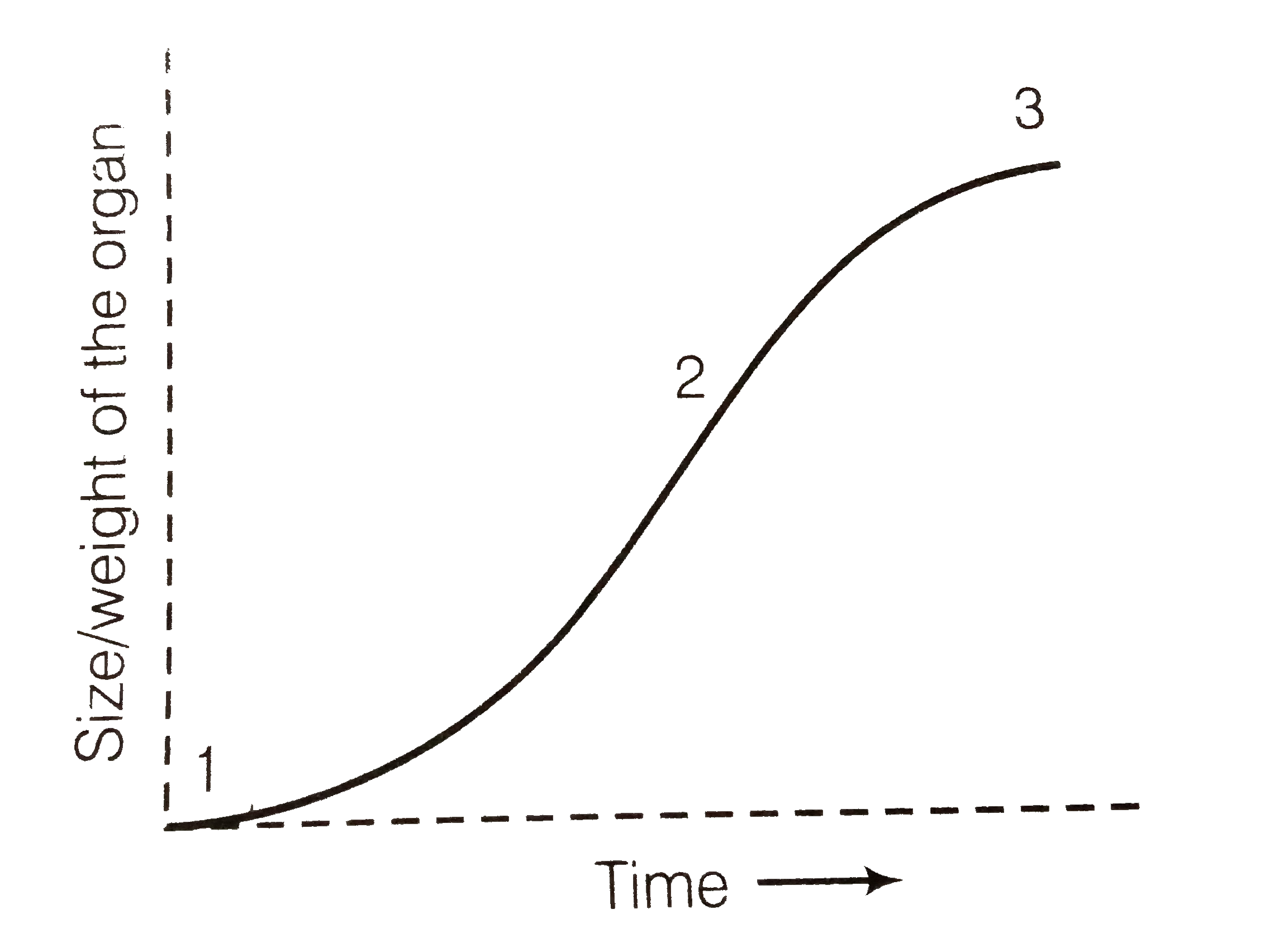
View SolutionWhat does the sigmoid growth curve of a population mean ?
View SolutionA sigmoid growth curve is characteristic of -
View SolutionThe number of death and birth in the last stage of sigmoid growth curve of a population will be
View Solution