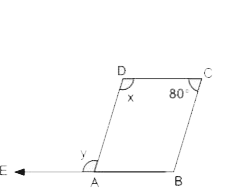
In the given figure, if ABCD is a parallelogram and E is the mid-point of BC, then ar (ΔDEC) = k ar(ABCD). Find the value of k.
A
2
B
14
C
12
D
23
Video Solution
Text Solution
The correct Answer is:B
|
Answer
Step by step video, text & image solution for In the given figure, if ABCD is a parallelogram and E is the mid-point of BC, then ar (DeltaDEC) = k ar(ABCD). Find the value of k. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- IMO QUESTION PAPER SET B 2019BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER SET B 2019EXERCISE - MATHEMATICAL REASONING
18 Videos
- IMO QUESTION PAPER SET B 2019BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER SET B 2019EXERCISE - EVERYDAY MATHEMATICS
10 Videos
- IMO QUESTION PAPER SET A 2019BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER SET A 2019EXERCISE - Achievers Section
5 Videos
- INTRODUCTION TO EUCLID'S GEOMETRYBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - Achievers Section (HOTS)
3 Videos
Similar Questions
Knowledge Check
In the given figure, ABCD is a parallelogram and M, N are the mid-points of AB and CD. The value of θ is
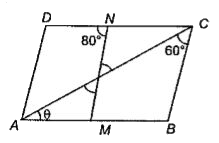 A20∘B30∘C40∘D10∘
A20∘B30∘C40∘D10∘In the given figure, ABCD is a parallelogram and M, N are the mid-points of AB and CD. The value of θ is
 A20*B30*C40*D10*
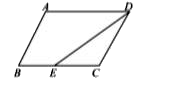
A20*B30*C40*D10*In the figure, ABCD and EFGD are two parallelograms and G is the mid-point of CD. Then, ar(ΔDPC)=ar(EFGD).
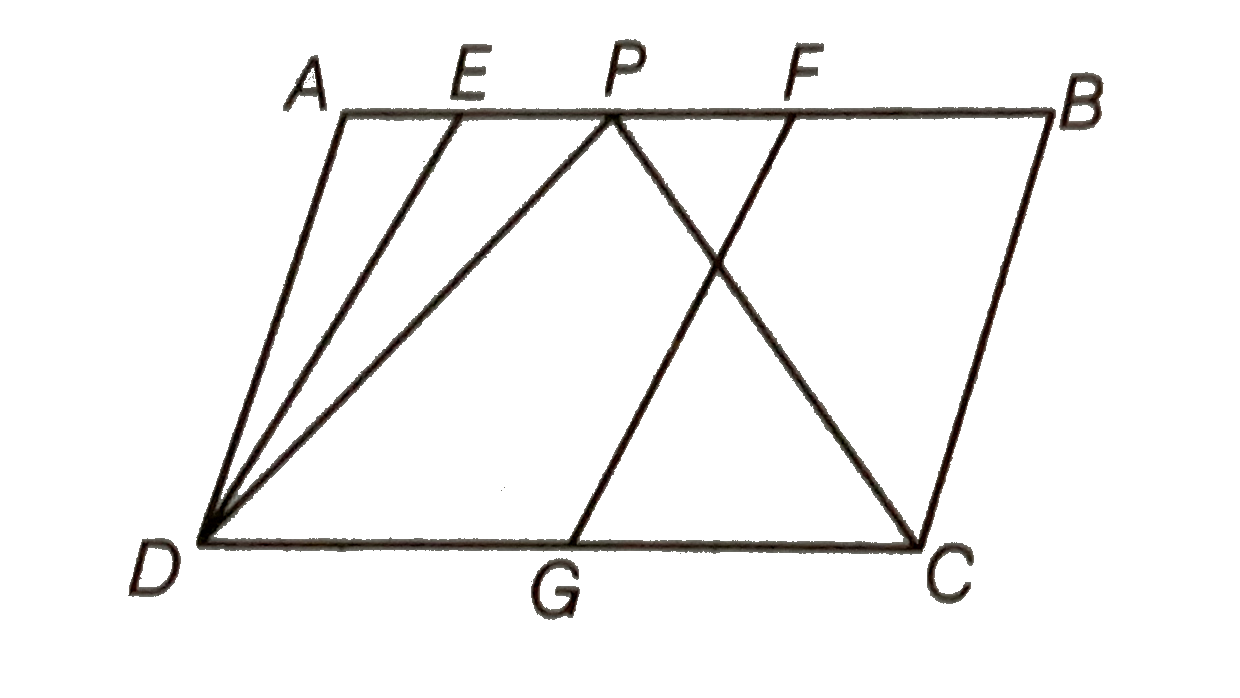 ATrueBFalseCPartially trueDNone of these
ATrueBFalseCPartially trueDNone of these
ABCD is a parallelogram and X is the mid-point of AB. (AXCD)=24cm2, then ar(ABC)=24cm2.
View SolutionIf ABCD is a parallelogram, E is the mid-point of AB and CE bisects ∠BCD, then ∠DEC is
View SolutionIn the following figure ,ABCD is a parallelogram . Find the value of r .
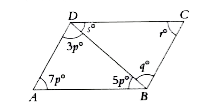
View SolutionIn parallelogram ABCD, if P is the mid-point of side AB, then
View SolutionABCD is a parallelogram and M is the mid point of BC. AB and DM are produced to meet at N, then :
View Solution