A particle of mass 'm' is projected with a velocity v=kVe(k<1) from the surface of the earth.(Ve = escape velocity)The maximum height above the surface reached by the particle is:
R(k1+k)2
R2k1+k
Rk21−k2
R(k1−k)2
The correct Answer is:C
−GmMR+12mv2=−GmMR+h
−GmMR+h=GmMR+12mk22GMR
−GmMR+h=GmMR(k2−1)
R+h=R1−k2
h=R[11−k2−1]=R[1−1+k21−k2]⇒h=Rk21−k2
Topper's Solved these Questions
- GRAVITATIONBOOK - ERRORLESSCHAPTER - GRAVITATIONEXERCISE - Assertion and Reason
25 Videos
- GRAVITATIONBOOK - ERRORLESSCHAPTER - GRAVITATIONEXERCISE - NCERT BASED QUESTIONS (Kepler’s Laws of Planetary Motion)
27 Videos
- FRICTION BOOK - ERRORLESSCHAPTER - FRICTION EXERCISE - ASSERTION & REASON
8 Videos
- KINETIC THEORY OF GASES BOOK - ERRORLESSCHAPTER - KINETIC THEORY OF GASES EXERCISE - ASSERTION AND REASON
16 Videos
Similar Questions
A particle of mass'm' is projected with velocity v0 at an angle 'α' with the horizontal. The coefficient of restitution for any of its impact with the smooth ground is e.
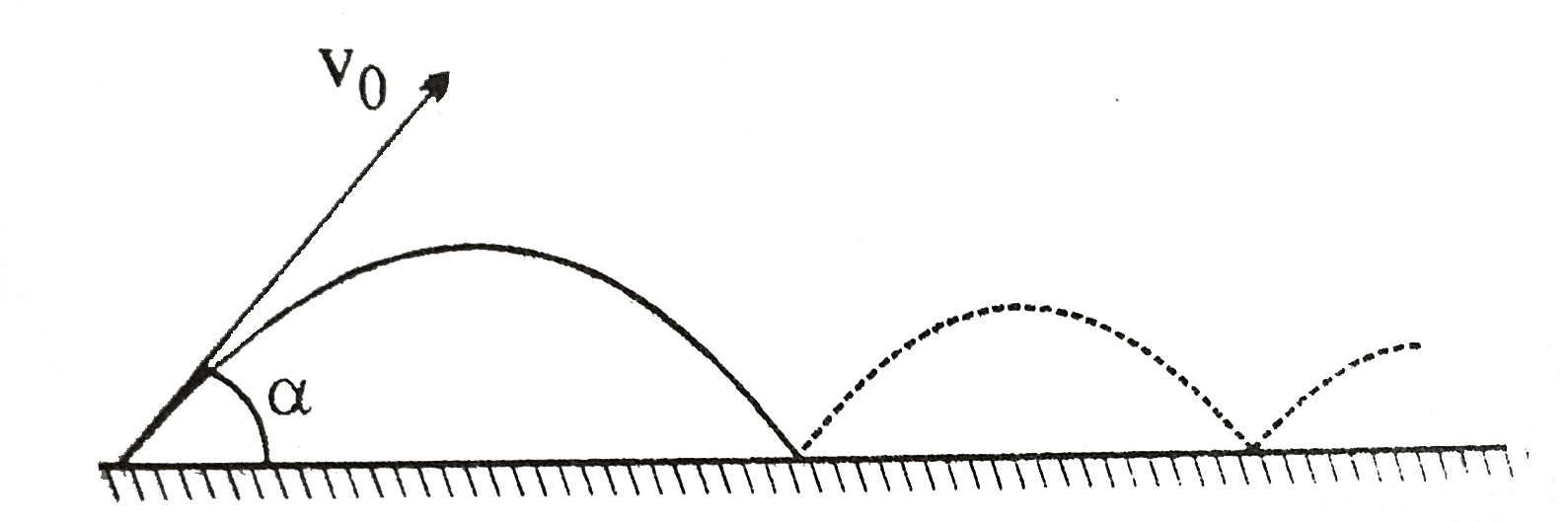
Find total time taken by the particle before it stops moving vertically?
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.
View Solution
Knowledge Check
A partricle of mass m is projected with a velocity v at an angle of 60∘ with horizontal When the particle is at the maximum height. The magnitude ofits angular momentum about the point ofprojection is
AzeroB3mv216gC√3mv316gD3mv316gA particle of mass m is projected with a velocity v making an angle of 45° with the horizontal. The magnitude of the angular momentum of the projectile about the point of projection, when the particle is at its maximum height h, is
AzeroBmv34√2gCmv3√2gDm√2gh3A particle of mass m is projected with a velocity v making an angle of 45∘ with the horizontal. The magnitude of the angular momentum of the projectile abut the point of projection when the particle is at its maximum height h is.
AzeroB(mv)34√2gC(mv)3√2gDm√2gh3
A particle of mass m is projected with a speed v0 at an angle of projection θ with horizontal. Find the torque of the weight of the particle about the point of projection after time v0sinθg
View SolutionA particle having mass m and charge q is projected with a velocity v making an angle q with the direction of a uniform magnetic field B. Calculate the magnitude of change in velocity of the particle after time t=πm2qB.
View SolutionA particle of mass m is projected with velocity making an angle of 45∘ with the horizontal When the particle lands on the level ground the magnitude of the change in its momentum will be .
View SolutionA particle of mass m is projected upword with velocity v=ve2 (ve) escape of the particle is
View SolutionA particle of mass m is projected upwards with velocity v=ve2, where ve is the escape velocity then at the maximum height the potential energy of the particle is : (R is radius of earth and M is mass of earth)
View Solution
