The gravitational force between a H-atom and another particle of mass m will be given by Newton's law
$F = G \frac{M . m}{r^{2}}$ where r is in m and

A

$M = m_{proton} + m_{electron}$

B

$M = m_{proton} + m_{electron} - \frac{B}{c^{2} (B = 13.6 e V)}$

C

M is not relate to the mass of the hydrogen atom

D

$M = m_{proton} + m_{electron} - \frac{| V |}{c^{2}}$ ( $| V |$ = magnitude of the potential energy of electron in the H-atom)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Given $F = \frac{G M m}{r^{2}}$
M = Effective mass of hydrogen atom
= Mass of electron + Mass of proton $- \frac{B}{c^{2}}$ where B is BE of hydrogen atom = 13 6. eV

|

Updated on:21/07/2023

Class 12 PHYSICS ATOMIC PHYSICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The gravitational force between a H-atom and another particle of mass m will be given by Newton's law: $F = G \frac{M . m}{r^{2}}$ , where r is in km and
A $M = m_{proton} + m_{electron}$
B $M = M_{proton} + m_{electron} - \frac{B}{c^{2}} (B = 13.6 e V)$
C $M$ is not related to the mass of the hydrogen atom
D $M = m_{proton} + m_{electron} - \frac{| V |}{c^{2}} (| V |)$ =magnitude of the potential energy of electron in the H-atom)
Question 2 - Select One
The gravitional force between two point masses $m_{1}$ and $m_{2}$ at separation $r$ is given by $F = k \frac{m_{1} m_{2}}{r^{2}}$
The constant $k$
ADepends on system of units only
BDepends on medium between masses only
CDepends on both (a) and (b)
DIs independent of both (a) and (b)
Question 3 - Select One
Assertion : Mass of the rod AB is $m_{1}$ and of particle P is $m_{2}$ . Distance between centre of rod and particle is r. Then the gravitational force between the rod and the particle is
$F = \frac{G m_{1} m_{2}}{r^{2}}$

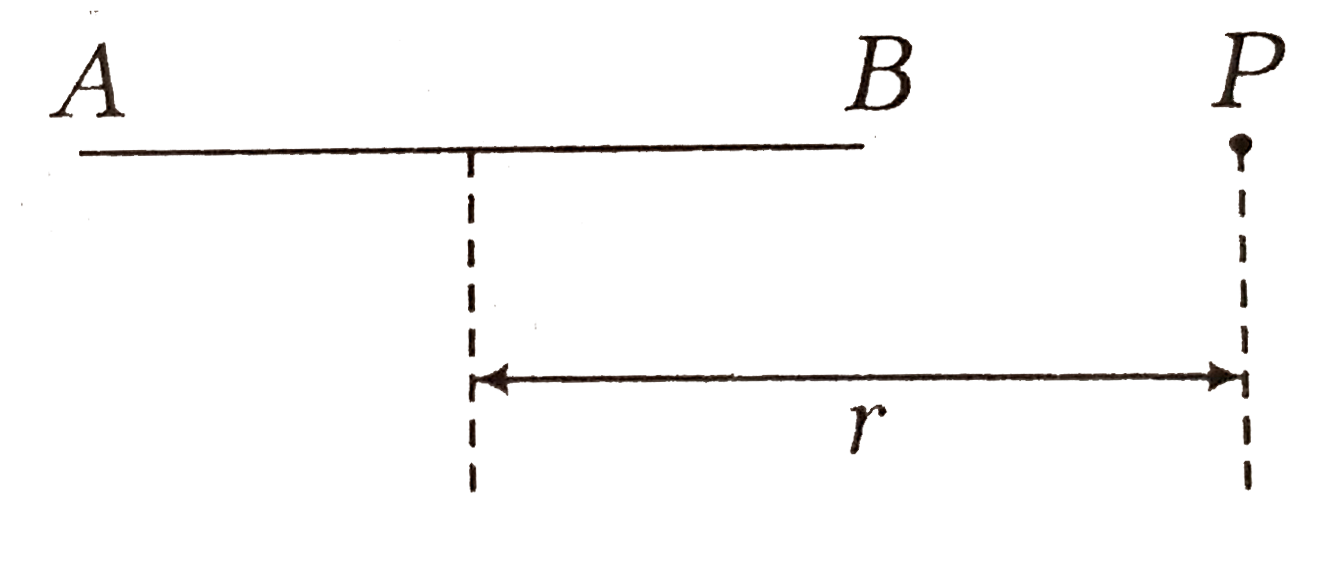
Reason : The relation $F = \frac{G m_{1} m_{2}}{r^{2}}$ can be applied directly only to find force between two particles.
AIf both Assertin and Reason are correct and Reason is the correct explanation of Assertion
BIf both Assertion and Reason are correct but Reason is not the correct explanation of Assertion
CIf Assertion is true but Reason is false
DIf Assertion is false but Reason is true

ERRORLESS-ATOMIC AND NUCLEAR PHYSICS-NCERT BASED QUESTIONS (Nucleus, Nuclear Reaction)

Home
Ask Doubt
Profile