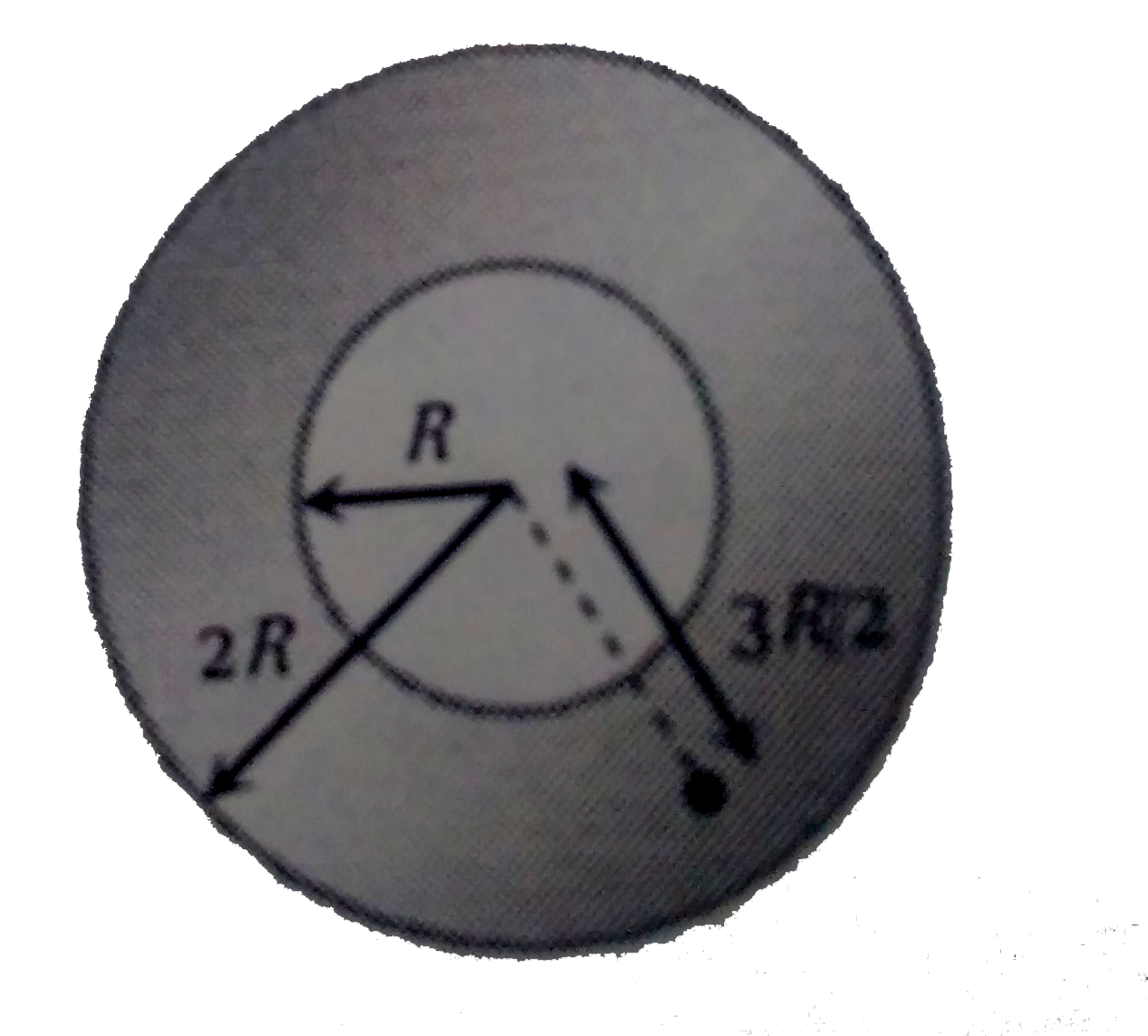
Figure shows the cross-sectional view of the hollow cylindrical conductor with inner radius 'R' and outer radius '2R', cylinder carrying uniformly distributed current along it's axis. The magnetic induction at point 'P' at a distance 3R2 from the axis of the cylinder will be
Zero
5μ0i72πR
7μ0i18πR
5μ0i36πR
The correct Answer is:A
By using B=μ0i2πr(r2−a2b2−a2) , here r=3R2 a = R , b = 2 R
We get B=μ02π(3R2)×(3R2)2−R2(2R)2−R2⎫⎪
⎪
⎪⎬⎪
⎪
⎪⎭=5μ0i36πR
Aliter : For R<x<2R
Current Inet=(iπ(2R)2−R2)[π(3R2)2−(R)2π]
= i3R2[9R24−R2]
=i3R2×5R24=5i12

Apply ampere circuit law - ∮B.dl=μ0Inet⇒B×2π3R2=μ05i12=5μ0i36πR
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT BOOK - ERRORLESSCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - NCERT BASED QUESTIONS (Motion of Charged Particle in Magnetic Field)
69 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - ERRORLESSCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - NCERT BASED QUESTIONS (Force and Torque on a Current Carrying Conductor )
51 Videos
- ELECTROSTATICSBOOK - ERRORLESSCHAPTER - ELECTROSTATICSEXERCISE - ASSERTION & REASON
25 Videos
- MAGNETISMBOOK - ERRORLESSCHAPTER - MAGNETISMEXERCISE - Assertion and Reason
22 Videos
Similar Questions
.Figure shows the cross-sectional view of the hollow cylindrical conductor with inner radius R and outer radius '2R',cylinder is carrying uniformly distributed current along it's axis.The magnetic induction at point p at a distance 3R2 from the axis of the cylinder will be 5μ0in×9πR .Find n?
View SolutionA hollow cylindrical conductor of inner radius a and outer radius b carries a current I uniformly spread over its cross-section. Find the magnetic field induction at a point inside the body of the conductor at a distance r [where a<r<b] from the axis of the cylinder.
View Solution
Knowledge Check
An infinitely long hollow conducting cylinder with inner radius r2 and outer radius R carries a uniform current ra density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
A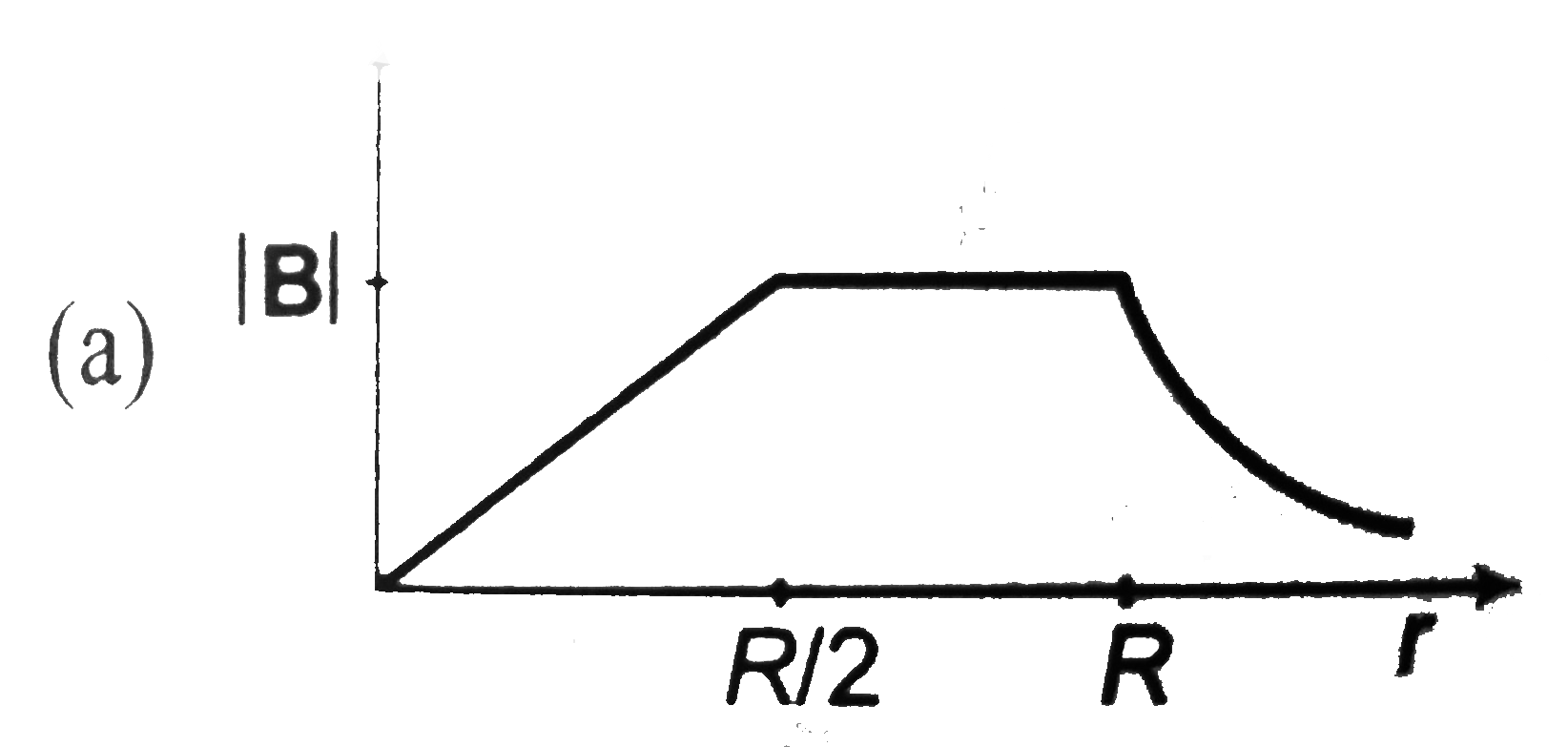 B
B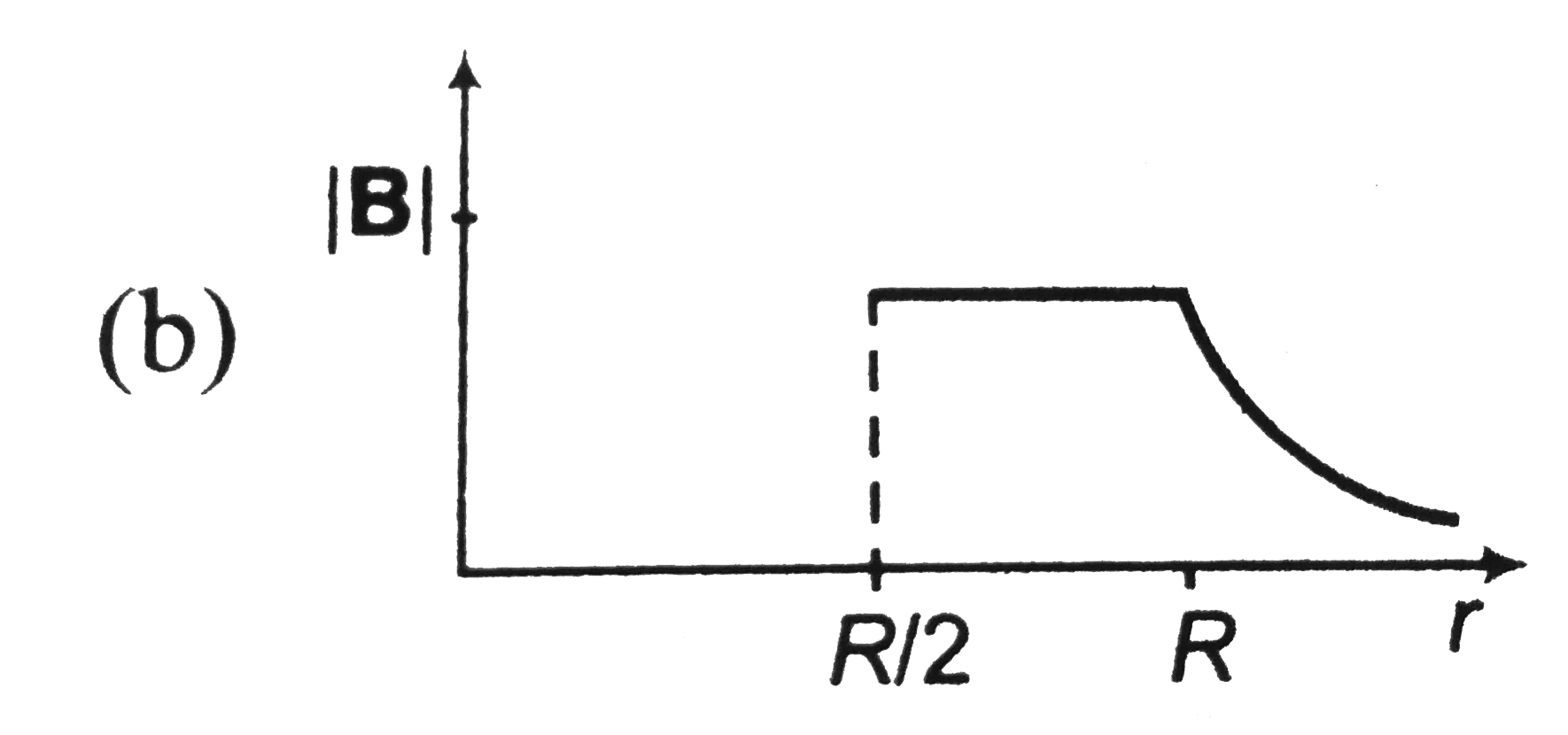 C
C D
D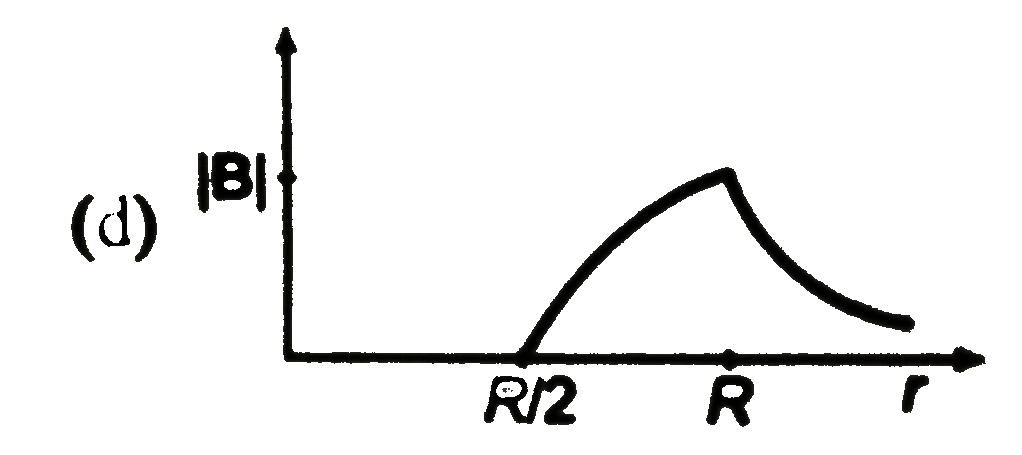
Axis of a solid cylinder of infinite length and radius R lies along y-axis. It carries a uniformly distributed current I along +y direction. Magnetic field at a point (R/2,y,R/2) is
Aμ0I4πR(ˆi−ˆk)Bμ0I2πR(ˆj−ˆk)Cμ0I4πRˆjDμ0I4πR(ˆi+ˆk)An infinitely long hollow conducting cylinder with inner radius R2 and outer radius R carries a uniform current ra density along its length . The magnitude of the magnetic field , ∣∣→B∣∣ as a function of the radial distance r from the axis is best represented by
A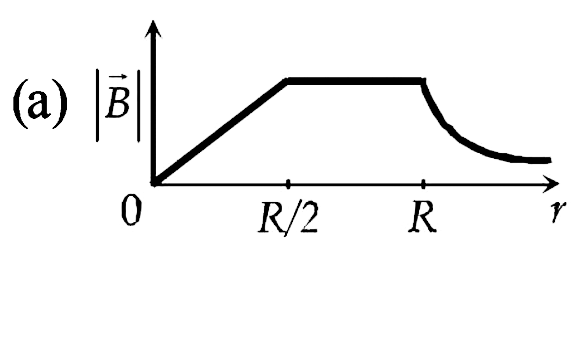 B
B C
C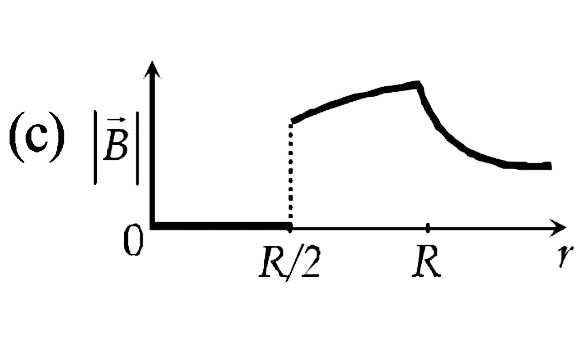 D
D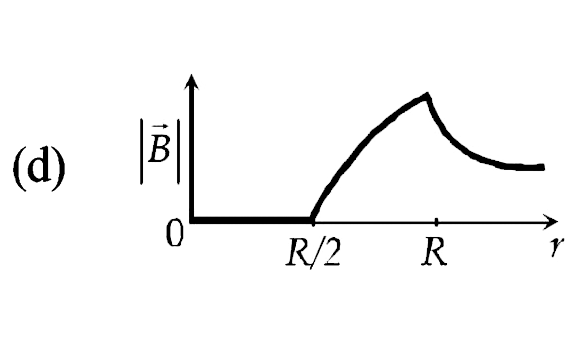
A solid cylinder carries current of 1 A uniformly distributed over its cross sectional area. Calculate the magnetic field induction at point P, at a distance of 3 cm from the axis of cylinder, if its radius is 7 cm .
View SolutionThe figure shows the cross-section of a long cylindrical conductor of radius a carrying a uniformly distributed current i. The magnetic field due to current at P is :
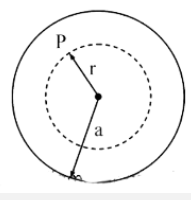
View SolutionA long straight solid metal rod of radius 4cm carries a current 2A, uniformly distributed over its circular cross-section. Find the magnetic field induction at a distance 3cm from the axis of the wire.
View SolutionA long thick conducting cylinder of radius 'R' carries a current uniformly distributed over its cross section :
View SolutionA thick current carrying cable of radius 'R' carries current 'I' uniformly distributed across its crosssection. The variation of magnetic field B(r) due to cable with distance 'r' from the axis of the cable is represented by.
View Solution
