If the velocity of a particle is v=At+Bt2, where A and B are constant, then the distance travelled by it between 1s and 2s is :
32A+4B
3A + 7B
32A+73B
A2+B3
The correct Answer is:C
V=At+Bt2⇒dxdt=At+Bt2
⇒∫x0dx=∫21(At+Bt2)dt=[At22+Bt33]21
⇒x=3A2+7B3
Topper's Solved these Questions
- MOTION IN ONE DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN ONE DIMENSIONEXERCISE - ASSERTION AND REASON
24 Videos
- MOTION IN ONE DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN ONE DIMENSIONEXERCISE - NCERT BASED QUESTIONS (MOTION UNDER GRAVITY )
56 Videos
- KINETIC THEORY OF GASES BOOK - ERRORLESSCHAPTER - KINETIC THEORY OF GASES EXERCISE - ASSERTION AND REASON
16 Videos
- MOTION IN TWO DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - ASSERTION & REASON
19 Videos
Similar Questions
The instantaneous velocity of a particle moving in a straight line is given as v=αt+βt2, where α and β are constants. The distance travelled by the particle between 1s and 2s is :
View SolutionThe velocity of a particle varies with time as per the figure shown. The distance travelled by the particle in 10 seconds is ?(m/s)
View Solution
Knowledge Check
If the velocity of a particle is v=At+Bt2, where A and B are constant, then the distance travelled by it between 1s and 2s is :
A32A+4BB3A+7BC32A+73BDA2+B3the velocity of a particle varies with time as shown below the distance travelled by the travelled by the particle during t=2s"and" t= 6s. Is
 A2πmB(2π+40)mC4πmD40m
A2πmB(2π+40)mC4πmD40m. If the velocity of a particle is (10 + 2 t 2) m/s , then the average acceleration of the particle between 2s and 5s is
A2m/s2B4m/s2C12m/s2D14m/s2
If velocity of a particle is v=bs2 ,where b is constant and s is displacement. The acceleration of the particle as function of s is?
View SolutionThe momentum of a particle is P=A+Bt2 . Where , A and B are constant perpendicular vectors . The force acting on the particle when its acceleration is at 45∘ with its velocity is
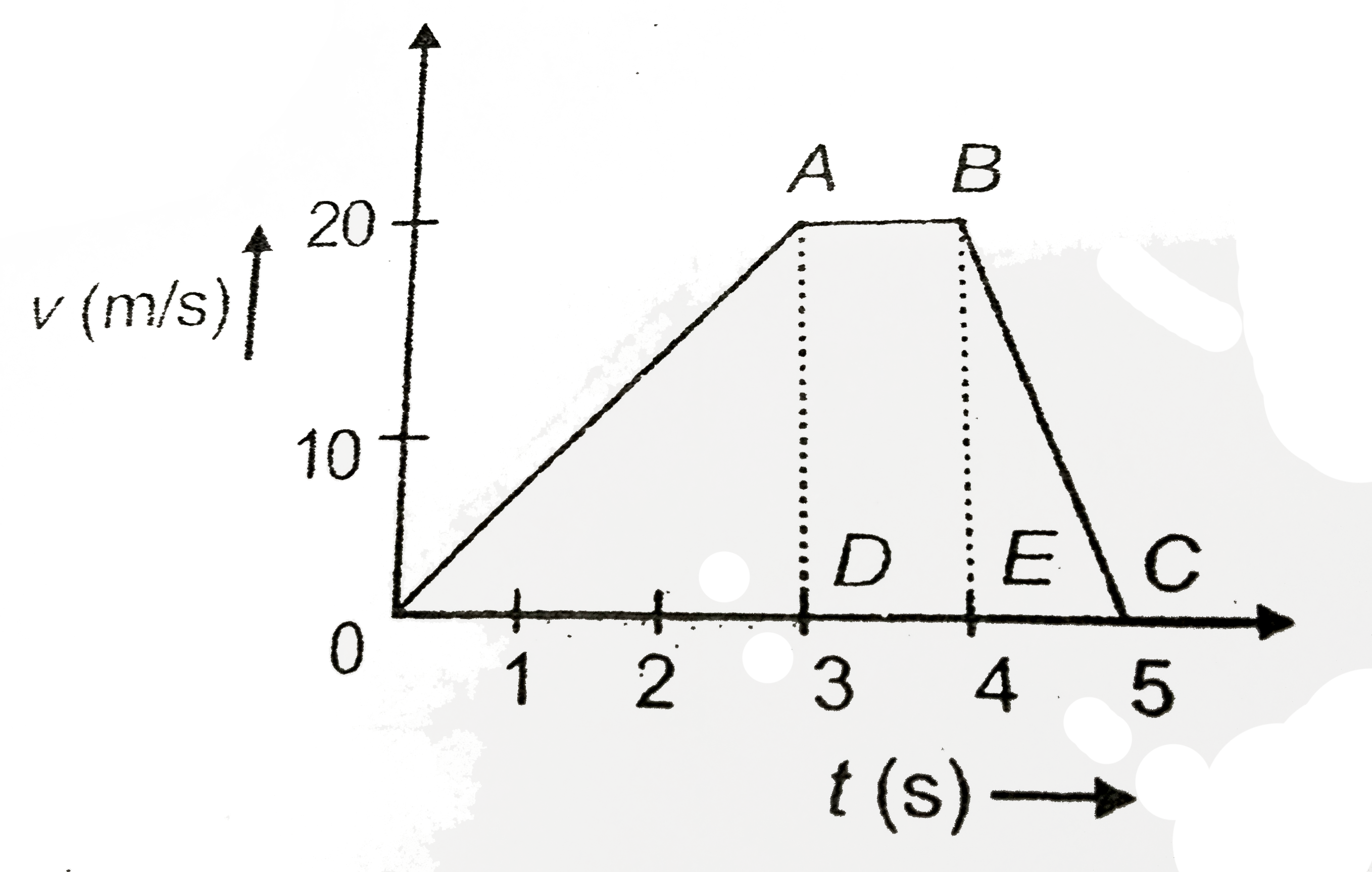
View SolutionThe variation of velocity of a particle moving along a straight line is as shown in the figure given below. The distance travelled by the particle in 5 s is
View SolutionThe position of a particle is given by
x=2(t−t2)
where t is expressed in seconds and x is in metre.
The total distance travelled by the paticle between t=0 to t=1s is
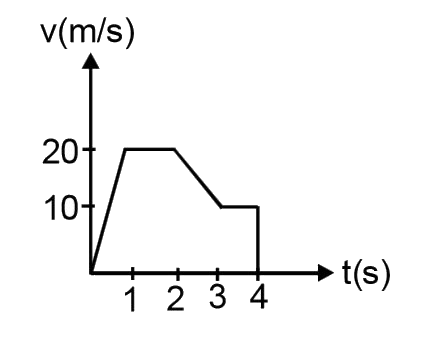
View SolutionThe variation of velocity of a particle moving along straight line is shown in the figure. The distance travelled by the particle in 4 s is
View Solution
