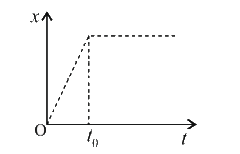
Figures (i) and (ii) below show the displacement-time graphs of two particles moving along the x -axis. We can say that
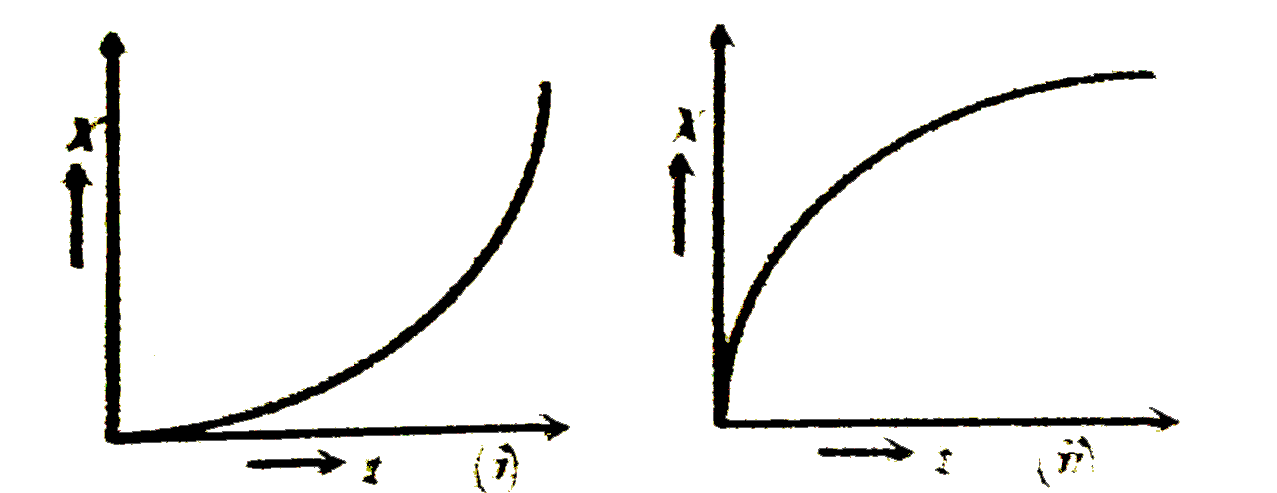
Both the particles are having a uniformly accelerated motion
Both the particles are having a uniformly retarded motion
Particle (i) is having a uniformly accelerated motion while particle (ii) is having a uniformly retarded motion
Particle (i) is having a uniformly retarded motion while particle (ii) is having a uniformly accelerated motion
The correct Answer is:C
(i) distance increases with time and slope increases (ii) Slope decreases with time and finally particle stop.
Topper's Solved these Questions
- MOTION IN ONE DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN ONE DIMENSIONEXERCISE - NCERT BASED QUESTIONS (RELATIVE MOTION )
18 Videos
- MOTION IN ONE DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN ONE DIMENSIONEXERCISE - NCERT BASED QUESTIONS (MOTION UNDER GRAVITY )
56 Videos
- MOTION IN ONE DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN ONE DIMENSIONEXERCISE - NCERT BASED QUESTIONS (UNIFORM MOTION )
24 Videos
- KINETIC THEORY OF GASES BOOK - ERRORLESSCHAPTER - KINETIC THEORY OF GASES EXERCISE - ASSERTION AND REASON
16 Videos
- MOTION IN TWO DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - ASSERTION & REASON
19 Videos
Similar Questions
Knowledge Check
Figure (i) and (i) show the displacement-time graphs of two particles moving along the x-axis. We can say that
 Aboth the particles are having a uniformly retarded motionBboth the particles are having a uniformly acceleraled motionCParticle (1) is having a uniformly accelerated motion while particle (i) is having a uniformly retarded motionDParticle (i) is having a uniformly retarded motion while particle (ii) is having a uniformly accelerated motion
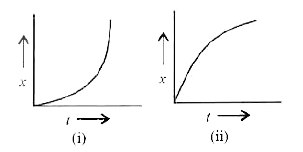
Aboth the particles are having a uniformly retarded motionBboth the particles are having a uniformly acceleraled motionCParticle (1) is having a uniformly accelerated motion while particle (i) is having a uniformly retarded motionDParticle (i) is having a uniformly retarded motion while particle (ii) is having a uniformly accelerated motionFigure show the displacement - time graph of a particle moving on the x-axis
 Athe particle is continuously going in positive X directionBthe particle is at restCthe velocity increases up to a time t0 and then becomes constant.Dthe particle moves at constant velocity up to a time t0 and then stops.
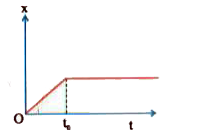
Athe particle is continuously going in positive X directionBthe particle is at restCthe velocity increases up to a time t0 and then becomes constant.Dthe particle moves at constant velocity up to a time t0 and then stops.The displacement-time graph of a particle is as shown below. It indicates that
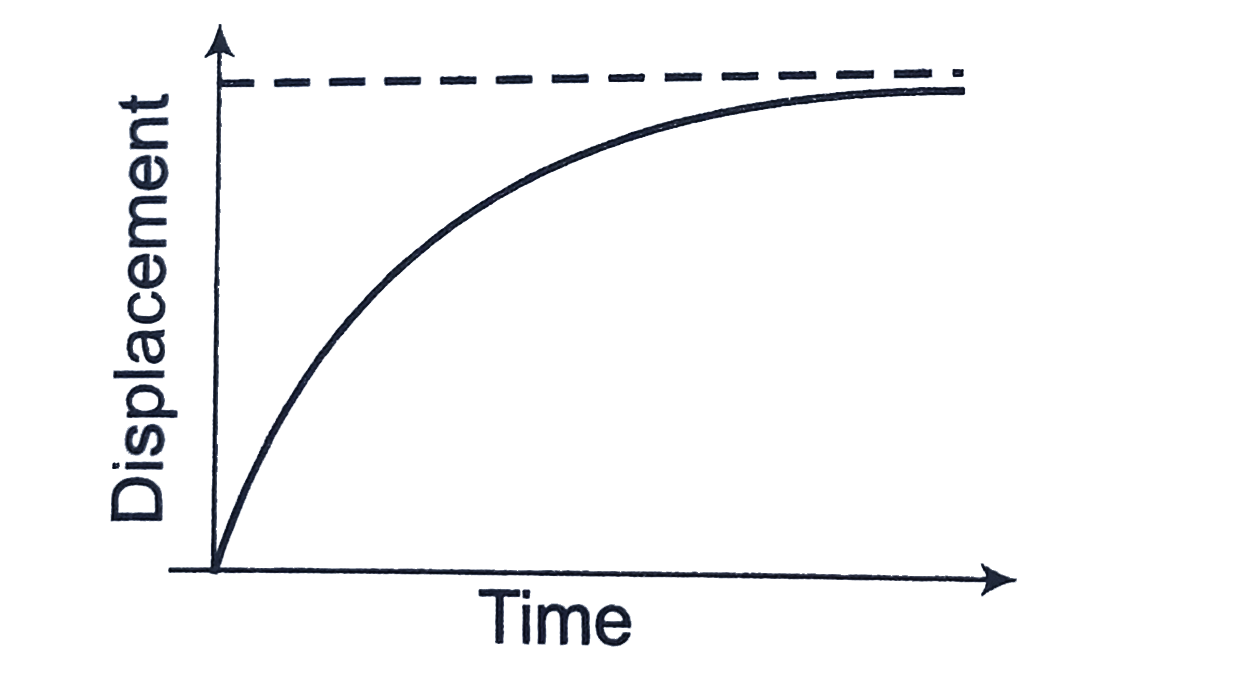 Athe particle starts with a certain velocity but the motion is retarded and finally the particle stopsBthe velocity of the particle is constant throufgoutCthe acceleration of the particle is constant throughoutDthe particle starts with a velocity, the motion is accelerated and finally the particle moves with a constant velocity
Athe particle starts with a certain velocity but the motion is retarded and finally the particle stopsBthe velocity of the particle is constant throufgoutCthe acceleration of the particle is constant throughoutDthe particle starts with a velocity, the motion is accelerated and finally the particle moves with a constant velocity
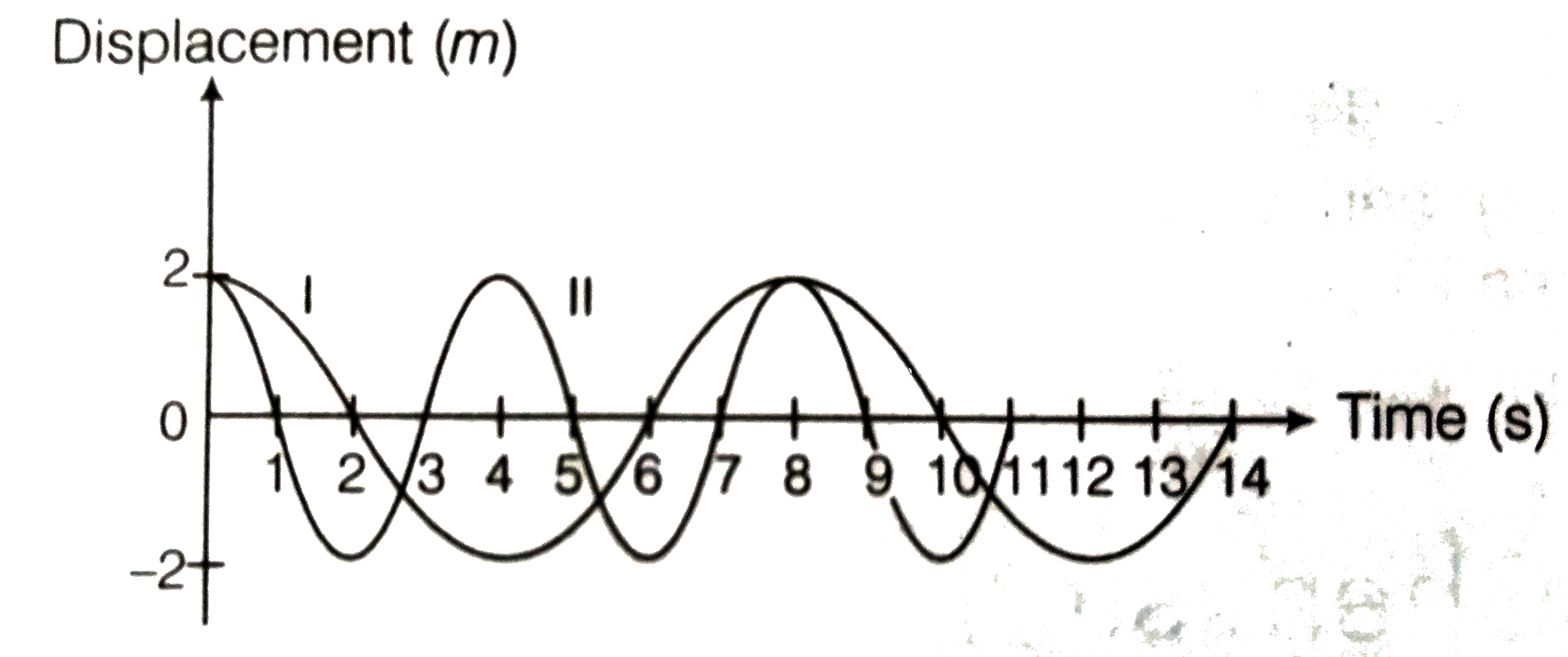
Figure shows the displacement time graphs of two simple harmonic motions I and II. From the graph it follows that
View SolutionDraw the acceleration-time graphs for the given velocity-time graphs of a particle moving along x-axis.

View SolutionDisplacement time graph of a particle moving in a straight line is a shown in figure.
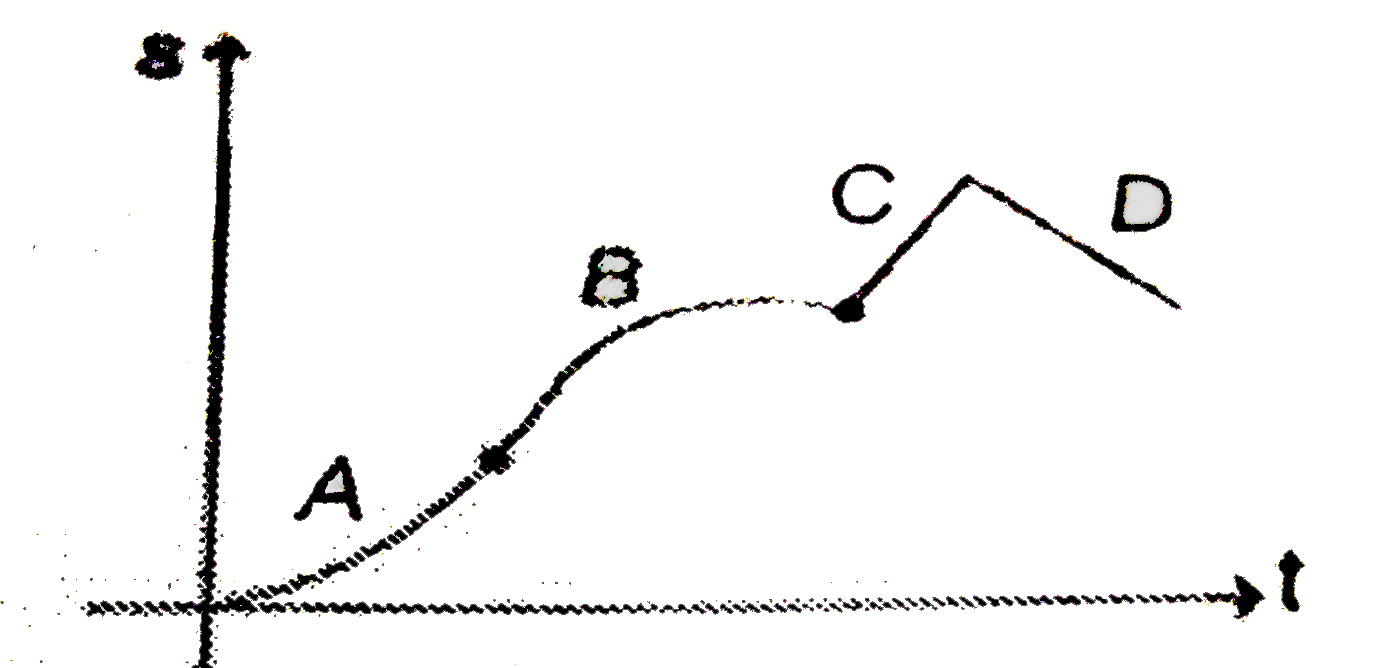
View SolutionIf the time-displacement graph of a particle is parallel to the-axis, the velocity of the particle is
View SolutionFigure shows two displacement-time graphs of particles P1 and P2
Their relative velocity is

View Solution