The displacement of a particle is moving by $x = {(t - 2)}^{2}$ where $x$ is in metres and $t$ in second. The distance covered by the particle in first $4$ seconds is.

A

4m

B

8m

C

12m

D

16m

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Given $x = {(t - 2)}^{2}$
$v = \frac{d x}{d t} = \frac{d}{d t} {(t - 2)}^{2} = 2 (t - 2) m / s$
$a = \frac{d v}{d t} = \frac{d}{d t} [2 (t - 2)]$
$= 2 [1 - 0] = 2 m / s^{2}$
when t = 0 , v = -4m/s
t = 2s , v = 0m/s
t = 4s, v = 4m/s

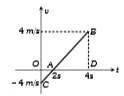
v-t graph is shown in adjacent diagram
Distance travelled = graph of the area
= Area OAC + Area ABD
$= \frac{4 \times 2}{2} + \frac{1}{2} \times 2 \times 4 = 8 m$

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The displacement of a particle is moving by $x = {(t - 2)}^{2}$ where $x$ is in metres and $t$ in second. The distance covered by the particle in first $4$ seconds is.
A4m
B8m
C12 m
D16 m
Question 2 - Select One
The position x of a particle varies with time t as $x = 6 + 12 t - 2 t^{2}$ where x is in metre and t is in seconds. The distance travelled by the particle in first five seconds is
A16 m
B26 m
C10 m
D36 m
Question 3 - Select One
The displacement of a particle moving in a straight line is described by the relation $s = 6 + 12 t - 2 t^{2}$ . Here $s$ is in metre and $t$ in second. The distance covered by the particle in first $5 s$ is
A $20 m$
B $32 m$
C $24 m$
D $26 m$

ERRORLESS-MOTION IN ONE DIMENSION-NCERT BASED QUESTIONS (NON-UNIFORM MOTION )

Home
Ask Doubt
Profile