A thin uniform rod of mass m and length l is hinged at the lower end to a level floor and stands vertically. It is now allowed to fall, then its upper end will strike the floor with a velocity given by
√2gl
√3gl
√5gl
√mgl
The correct Answer is:B
To solve the problem of a thin uniform rod of mass m and length l that is hinged at one end and allowed to fall, we will use the principle of conservation of energy. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Initial and Final States
Initially, the rod is vertical, and all its potential energy is due to its height. When it falls, it rotates about the hinge, and when it strikes the floor, its potential energy is converted into rotational kinetic energy.
Step 2: Calculate the Initial Potential Energy
The center of mass of the rod is at a height of l2 from the ground. The potential energy (PE) at this position is given by:
PEinitial=mgh=mg(l2)=mgl2
Step 3: Calculate the Final Kinetic Energy
When the rod strikes the floor, all the potential energy has been converted into rotational kinetic energy (KE). The rotational kinetic energy of a rigid body is given by:
KEfinal=12Iω2
where I is the moment of inertia of the rod about the hinge and ω is the angular velocity.
Step 4: Find the Moment of Inertia
The moment of inertia I of a thin rod about one end is given by:
I=13ml2
Step 5: Relate Angular Velocity to Linear Velocity
The relationship between the linear velocity v of the upper end of the rod and the angular velocity ω is given by:
v=ωl⇒ω=vl
Step 6: Set Up the Energy Conservation Equation
Using conservation of energy:
PEinitial=KEfinal
Substituting the expressions we derived:
mgl2=12(13ml2)(vl)2
Step 7: Simplify the Equation
Cancelling m from both sides and simplifying:
gl2=16lv2
Multiplying both sides by 6:
3gl=lv2
Dividing both sides by l:
3g=v2
Step 8: Solve for Velocity
Taking the square root of both sides gives:
v=√3g
Conclusion
The velocity of the upper end of the rod when it strikes the floor is:
v=√3g
Initially, the rod is vertical, and all its potential energy is due to its height. When it falls, it rotates about the hinge, and when it strikes the floor, its potential energy is converted into rotational kinetic energy.
The center of mass of the rod is at a height of l2 from the ground. The potential energy (PE) at this position is given by:
PEinitial=mgh=mg(l2)=mgl2
When the rod strikes the floor, all the potential energy has been converted into rotational kinetic energy (KE). The rotational kinetic energy of a rigid body is given by:
KEfinal=12Iω2
where I is the moment of inertia of the rod about the hinge and ω is the angular velocity.
The moment of inertia I of a thin rod about one end is given by:
I=13ml2
The relationship between the linear velocity v of the upper end of the rod and the angular velocity ω is given by:
v=ωl⇒ω=vl
Using conservation of energy:
PEinitial=KEfinal
Substituting the expressions we derived:
mgl2=12(13ml2)(vl)2
Cancelling m from both sides and simplifying:
gl2=16lv2
Multiplying both sides by 6:
3gl=lv2
Dividing both sides by l:
3g=v2
Taking the square root of both sides gives:
v=√3g
The velocity of the upper end of the rod when it strikes the floor is:
v=√3g
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Rolling on Inclined Plane)
54 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - PAST YEARS QUESTIONS
70 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESSCHAPTER - ROTATIONAL MOTIONEXERCISE - NCERT BASED QUESTIONS (Angular Momentum)
52 Videos
- NEWTON'S LAWS OF MOTIONBOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON
18 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESSCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assertion & Reason
15 Videos
Similar Questions
A thin uniform rod AB of mass m and length l is hinged at one end to the level floor and stands vertically. If it s allowed to fall, with what angular velocity will it strike the floor?
View SolutionA uniform stick of mass M and length L is kept vertical on a frictionless horizontal floor. If the stick is allowed to fall, then mark the correct alternatives
View Solution
Knowledge Check
A thin rod of mass m and length l is hinged at the lower end to a level floor and stands vertically. Then its upper end will strike the floor with a velocity given by:
A√2glB√3glC√5glD√mglA thin uniform rod of length l is pivoted at its upper end. It is free to swing in a vertical plane. Its time period for oscillation of small amplitude is
A2π√lgB2π√2l3gC2π√3l2gD2π√l3gA rod of length L, hinged at the bottom is held vertically and then allowed to fall, the linear velocity of its top when it hits the floor is
A√2gLB√2gLC√3gLD√3gL
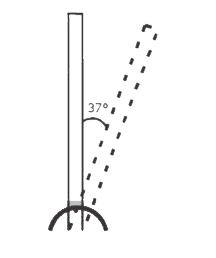
A uniform rod of mass M & length L is hinged about its one end as shown. Initially it is held vartical and then allowed to rotate, the angular velocity of rod when it makes an angle of 37∘ with the vertical is
View SolutionA uniform rod of mass M and length L is hinged at its lower end on a table. The rod can rotate freely in vertical plane and there is no friction at the hinge. A ball of mass M and radius R=L3 is placed in contact with the vertical rod and a horizontal force F is applied at the upper end of the rod.
(a) Find the acceleration of the ball immediately after the force starts acting.
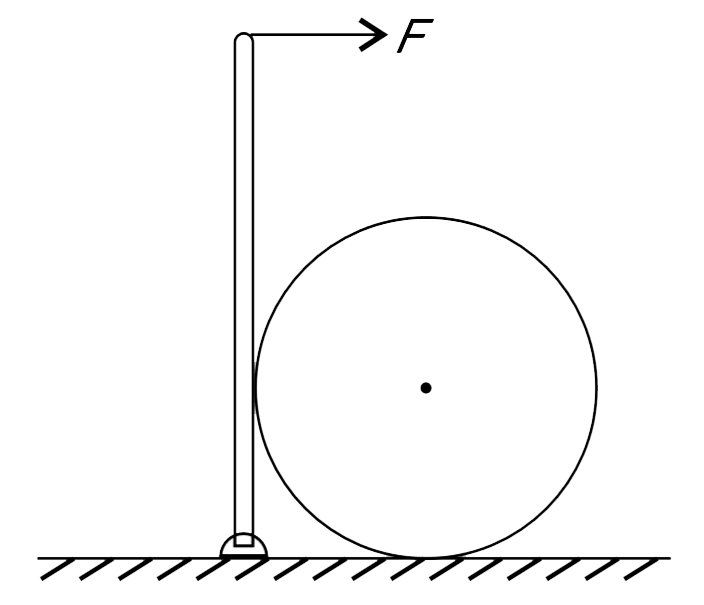
(b) Find the horizontal component of hinge force acting on the rod immediately after force F starts acting.
View SolutionA thin uniform rod of mass m and length l, pivoted freely at its base, is allowed to fall from a vertical position. Calcualte its angular velocity and acceleration when it has turned through 60∘.
View SolutionA uniform rod of mass m and length l is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity v0 collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
View SolutionA thin uniform rod of mass m and length l is free to rotate about its upper end. When it is at rest, it receives an impulse J at its lowest point, normal to its length. Immediately after impact,
View Solution
