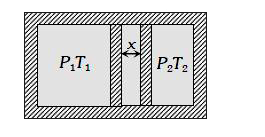
Following figure shows on adiabatic cylindrical container of volume V0 divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas (Cp/Cy=λ) is at pressure P1 and temperature T1 in left part and gas at pressure P2 and temperature T2 in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (Suppose x = displacement of the piston)

P2
P1
P1(V02)γ(V02+Ax)γ
P2(V02)γ(V02+Ax)γ
The correct Answer is:C
Final volume of the left and right part
VL=V02+Ax
VR=V02−Ax
Since, container wall and piston are adiabatic in left side and gas undergoes adiabatic expansion on right side the gas undergoes adiabatic compression.
P1(V02)γ=Pγf(V02+Ax) (for left side)
P2(V02)γ=Pγf(V02−Ax) (for right side)
∴P1P2=(V02+Ax)γ(V02−Ax)γ⇒Ax=V02[P1/γ1−P1/γ2][P1/γ1+P1/γ2]
Now, Pf=P1(V02)γ[V02+Ax]γ
Topper's Solved these Questions
- THERMODYNAMICSBOOK - ERRORLESSCHAPTER - THERMODYNAMICSEXERCISE - NCERT BASED QUESTIONS (ISOBARIC AND ISOCHORIC PROCESS)
10 Videos
- THERMODYNAMICSBOOK - ERRORLESSCHAPTER - THERMODYNAMICSEXERCISE - NCERT BASED QUESTIONS (HEAT ENGINE, REFRIGERATOR AND SECOND LAW OF THERMODYNAMICS)
35 Videos
- THERMODYNAMICSBOOK - ERRORLESSCHAPTER - THERMODYNAMICSEXERCISE - NCERT BASED QUESTIONS (ISOTHERMAL PROCESS)
16 Videos
- SURFACE TENSIONBOOK - ERRORLESSCHAPTER - SURFACE TENSIONEXERCISE - ASSERTION & REASON
11 Videos
- THERMOMETRY, THERMAL EXPANSION AND CALORIMETRYBOOK - ERRORLESSCHAPTER - THERMOMETRY, THERMAL EXPANSION AND CALORIMETRYEXERCISE - ASSERTION & REASON
10 Videos
Similar Questions
In given figure, an adiabatic cylindrical tube of volume 2V0 is divided in two equal parts by a frictionless adiabatic separator. An ideal gas in left side of a tube having pressure P1 and temperature T1 where as in the right side having pressure P2 and temperature T2.Cp/Cv=γ is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the final volumes of the two parts (b) the heat given to the gas in the left part and (c) the final common pressure of the gases,
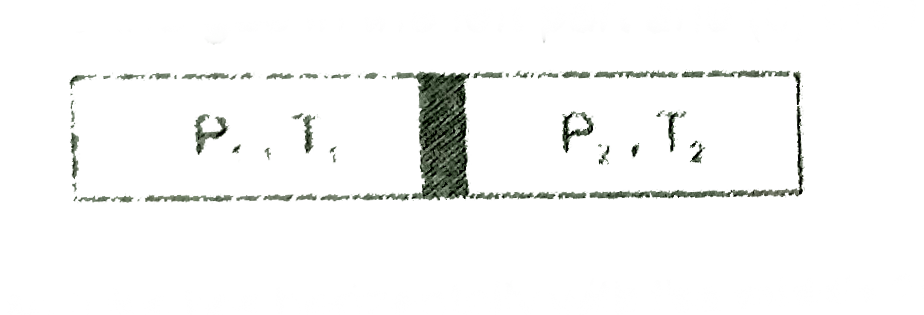
View SolutionFigure shows an adiabatic cylindrical tube of volume (V0) divided in two parts by a frictionless adibatic separator . Initially, the separator is kept in the middle, an ideal gas at pressure (p1) and the temperatures (T1) is injected into the left part and the another ideal gas at pressures (P2) and temperature (T2) is injected into the right part. (CpCv=γ) is the same for both the gases. The separator is slid slowly and is released at a position where it can stay in equilibrium. Find (a) the volumes of the parts, (b) the heat given to the gas in the left part and (c) the final common pressure of the gases.

View Solution
Knowledge Check
Following figure shows on adiabatic cylindrical container of volume V0 divided by an adiabatic smooth piston (area of cross-section = A ) in two equal parts. An ideal gas (Cp/Cy=λ) is at pressure P and temperature T in left part and gas at pressure P and temperature T in right part. The piston is slowly displaced and released at a position where it can stay in equilibrium. The final pressure of the two parts will be (Suppose x = displacement of the piston)
 AP2BP1CP1(V02)λ(V02+Ax)λDP2(V02)λ(V02+Ax)λ
AP2BP1CP1(V02)λ(V02+Ax)λDP2(V02)λ(V02+Ax)λAn insulated container of gas has two chambers separated by an insulating partition. One of the chmabers has volume V1 and contains ideal gas at pressure P1 and temperature T1.The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
A(T1T2P1V1+P2V2P1V1T2+P2V2T1BP1V1T1+P2V2T2P1V1+P2V2CP1V1T2+P2V2T1P1V1+P2V2DT1T2(P1V1+P2V2)P1V1T1+P2V2T2An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1. The other chambers has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partion is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
AT1T2(P1V1+P2V2)P1V1T2+P2V2T1BP1V1T1+P2V2T2P1V1+P2V2CP1V1T2+P2V2T1P1V1+P2V2DT1T2(P1V1+P2V2)P1V1T1+P2V2T2
Show a cylindrical tube of volume V_(0) divided in two parts by a frictionless separator. The walls of the tube are adiabatic but the separator is conducting, Ideal gases ate filled in the two parts. When the swparator is kept in the middle, the pressure are p_(1) and p-(2) in the left part and the right part respectively. The separator is slowly slid and is released at a position where it can stay in equilibrium. Find the volumes if the two parts. (figure)
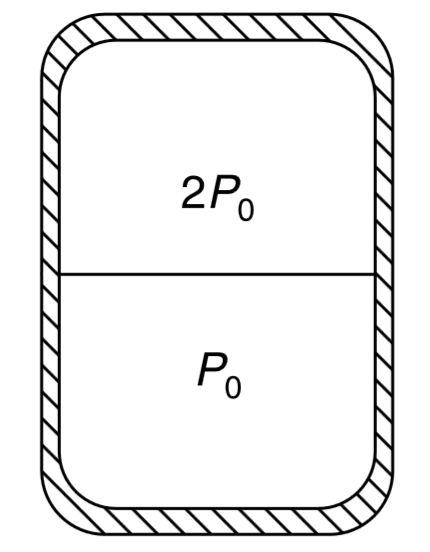
View SolutionA cylindrical container of volume V0 is divided into two parts by a thin conducting separator of negligible mass. The walls of the container are adiabatic. Ideal gases are filled in the two parts such that the pressures are P0 and 2P0 when the separator is held in the middle of the container (see figure). Now the separator is slowly slid and released in a position where it stays in equilibrium. Find the volume of the two parts.
View SolutionA diathermic piston divides adiabatic cylinder of volume V0 into two equal parts as shown in the figure. Both parts contain ideal monoatomic gases. The initial pressure and temperature of gas in left compartment are P0 and T0 while that in right compartment are 2P0 and 2T0. Initially the piston is kept fixed and the system is allowed to acquire a state of thermal equilibrium.
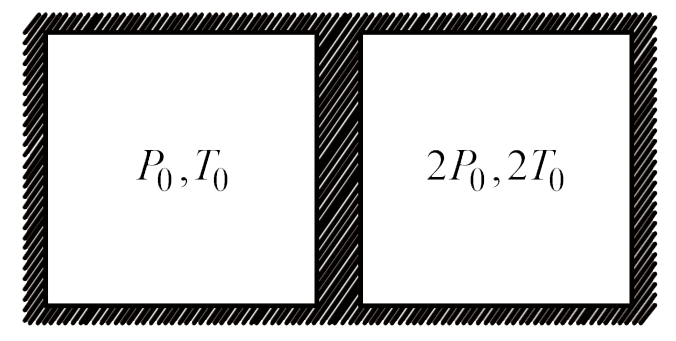
The pressure in left compartment after thermal equilibrium is achieved is
View SolutionOne mole of an ideal gas (Cp/Cv=γ) at absolute temperature T1 is adiabatically compressed from an initial pressure P1 to a final pressure P2. The resulting temperature T2, of the gas is given by:
View SolutionIn an adiabatic change, the pressure p and temperature T of a diatomic gas are related by the relation p∝Tα, where α equals
View Solution
