A vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring, so that the spring is compressed by a distance d. The net work done in the process is
mg(h+d)+12Kd2
mg(h+d)−12Kd2
mg(h−d)−12Kd2
mg(h−d)+12Kd2
The correct Answer is:B
Energy is conserved –
mg(h+d)=12kd2
Wnet=mg(h+d)−12kd2=0
Topper's Solved these Questions
- WORK, ENERGY POWER AND COLLISIONBOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - ASSERTION & REASON
22 Videos
- WORK, ENERGY POWER AND COLLISIONBOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - NCERT BASED QUESTIONS (Perfectly Inelastic Collision)
9 Videos
- WAVES AND SOUND BOOK - ERRORLESSCHAPTER - WAVES AND SOUND EXERCISE - ASSERTION & REASON
25 Videos
Similar Questions
A ball of mass m is droppped from a height h on a platform fixed at the top of a vertical spring. The platform is depressed by a distance x. What is the spring constant K?
View SolutionFigure. shows a rough horizontal plane which ends in a vertical wall, to which a spring is connected, having a force constant k. Initially spring is in its relaxed state. A block of mass m starts with an initial velocity u towards the spring from a distance l0 from the end of spring shown. When block strikes at the end ofthe spring, it compresses the spring and comes to rest. Find the maximum compression in the spring. The friction coefficient between the block and the floor is μ..
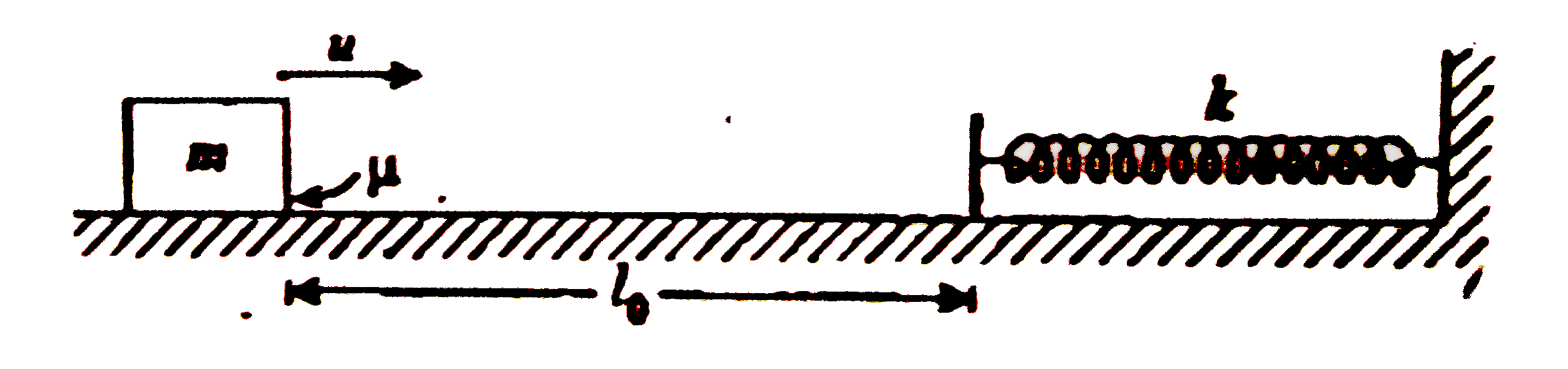
View Solution
Knowledge Check
A ball of mass m is dropped from a heighth on a platform fixed at the top of a vertical spring, as shown in figure. The platform is depressed by a distance x. Then the spring constant is
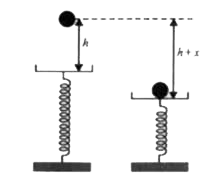 Amg(h+x)Bmg(h+2x)C2mg(h+x)x2Dmg(2h+x)
Amg(h+x)Bmg(h+2x)C2mg(h+x)x2Dmg(2h+x)A massless spring of length l and spring constant k is placed vertically on a table. A ball of mass m is just kept on top of the spring. The maximum velocity of the ball is
Ag√mkBg√2mkCg2√mkDg√m2kA spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
Av√(mk)Bmv√kCm√(vk)Dk√(mv)
A spring is compressed by 10 cm by a ball of mass 20 g . What will be the potential energy of a spring if the force constant of the spring is 20 N cm−1 .
View SolutionA spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring,pulled sideways to a distance of 2 cm and released . The speed of the mass when the spring is compressed by 1 cm is
View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a blcok of mass m resting on a smooth horizontal surface. There is another wall at distance x0 from the block. The spring is then compressed by 2x0 and released. The time taken to strike the wall is

View Solution
A spring having a spring constant k is fixed to a vertical wall as shown in Fig. A block of mass m moves with velocity v torards the spring from a parallel wall opposite to this wall. The mass hits the free end of the spring compressing it and is decelerated by the spring force and comes to rest and then turns the spring is decelerated by the spring force and comes to rest and then turns back till the spring acquires its natural length and contact with the spring is broken. In this process, it regains its angular speed in the opposite direction and makes a perfect elastice collision on the opposite left wall and starts moving with same speed as before towards right. The above processes are repeated and there is periodic oscillation.
Q. What is the time period of oscillation ?
View SolutionA force of 10 N holds an ideal spring with a 20Nm spring constant in compression. The potential energy stored in the spring is
View Solution
