Figure below shows a small mass connected to a string, which is attached to a vertical post. If the ball is released when the string is horizontal as shown, the magnitude of the total acceleration (including radial and tangential) of the mass as a function of the angle is

The correct Answer is:D
Radial acceleration =
Tangential acceleration
Total acceleration
Topper's Solved these Questions
- BOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - NCERT BASED QUESTIONS (Power)18videos
WORK, ENERGY POWER AND COLLISION
- BOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - NCERT BASED QUESTIONS (Elastic and Inelastic Collision)44videos
WORK, ENERGY POWER AND COLLISION
- BOOK - ERRORLESSCHAPTER - WORK, ENERGY POWER AND COLLISIONEXERCISE - NCERT BASED QUESTIONS (Work Done by Variable Force)26videos
WORK, ENERGY POWER AND COLLISION
- BOOK - ERRORLESSCHAPTER - WAVES AND SOUND EXERCISE - ASSERTION & REASON25videos
WAVES AND SOUND
Similar Questions
A ball A of mass m attached to a string of length L is released when the string is horizontal. It strikes another ball B of mass 2m suspended to another string of length L at rest as shown. Find the maximum angle made by the string if the collision is completely inelastic.
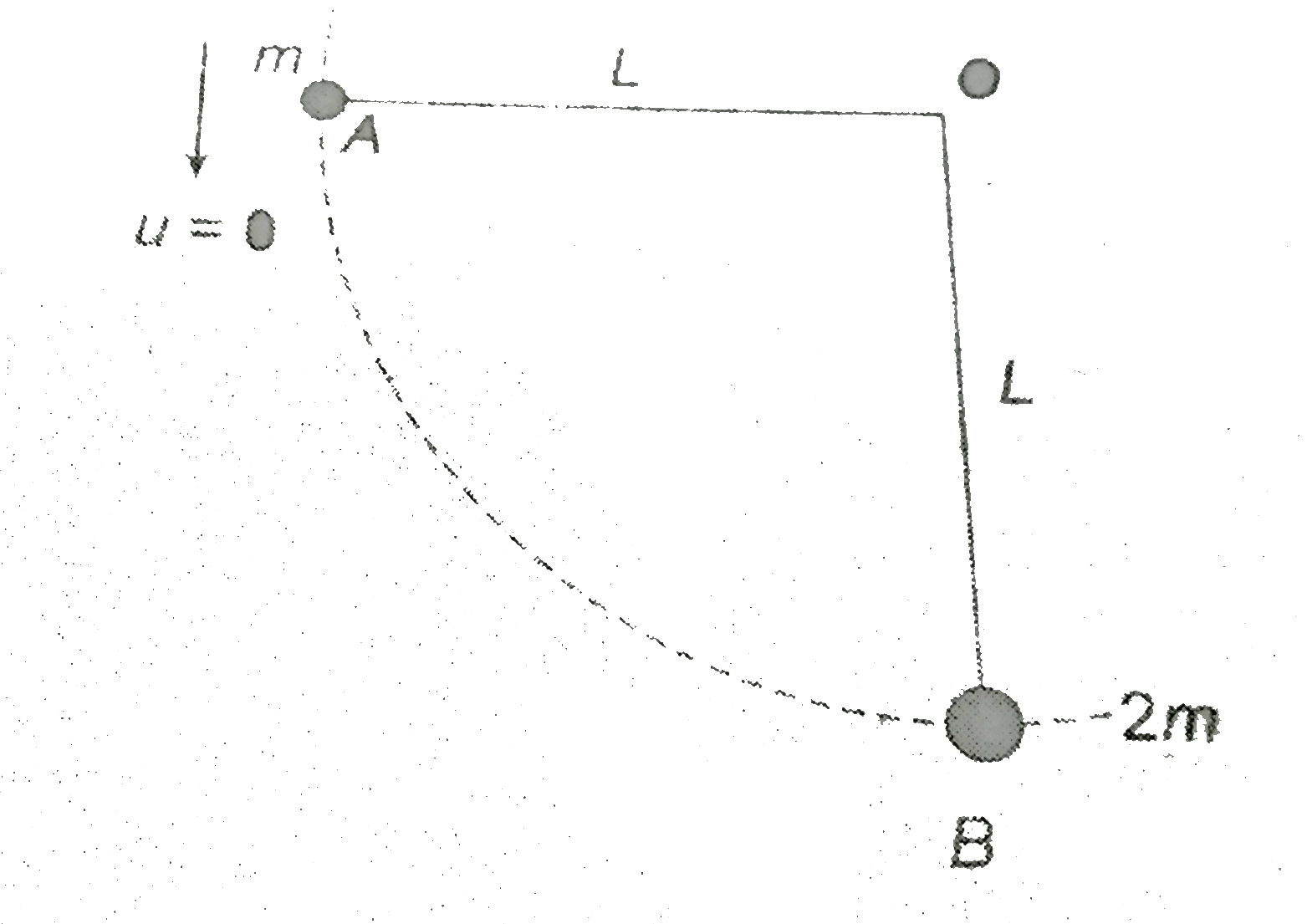 View Solution
View SolutionA ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut.
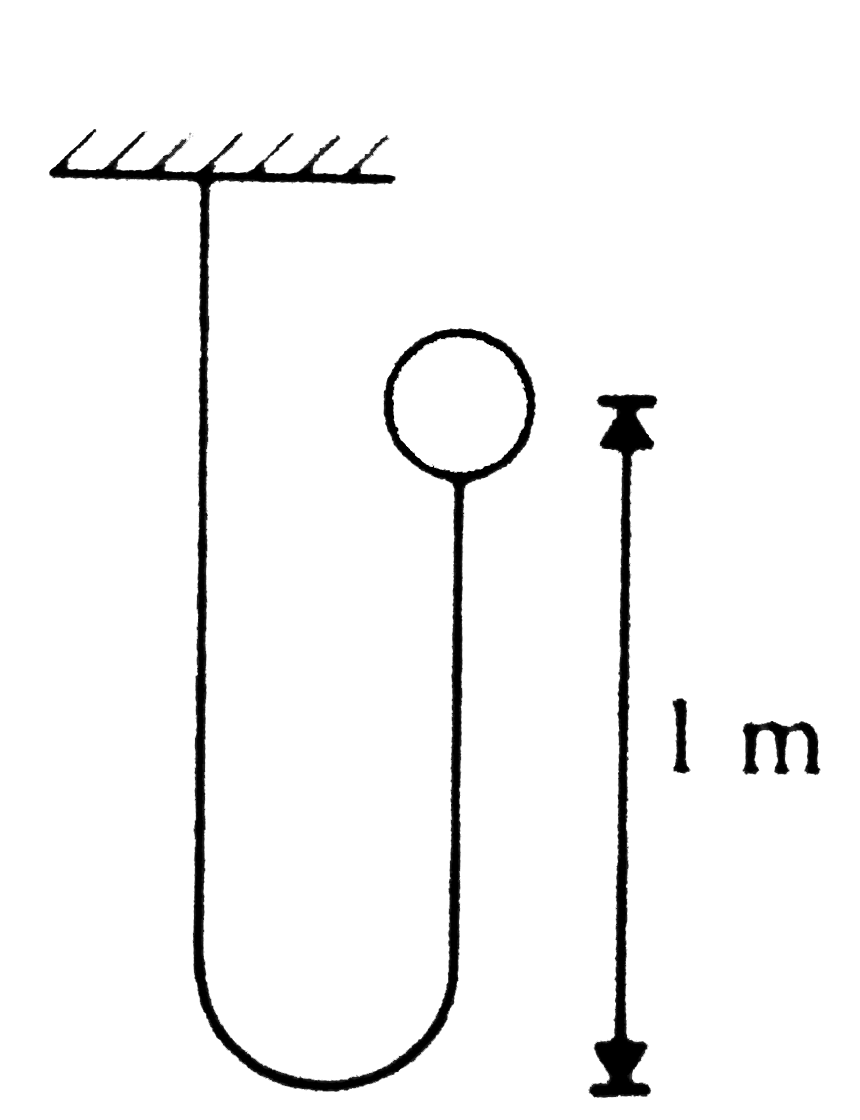 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The given figure shows a small mass connected to a string which is atteched to a string , which is attached to a vertical post. If the mass is released from rest when the string is horizontal as shown the magnitude of the total acceleration of the mass as friction of the angle θ is
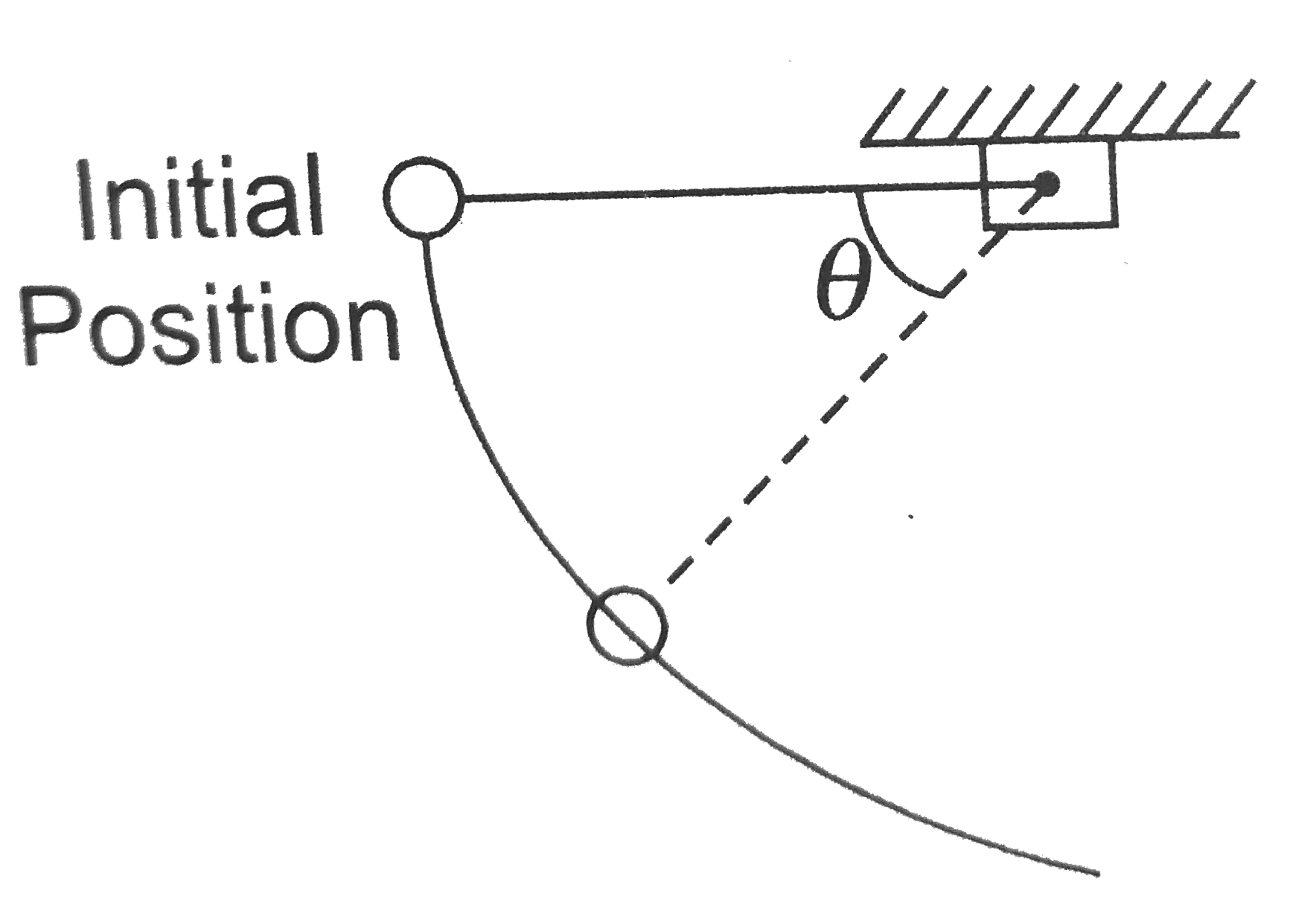 A2gsinθB2gcosθCg√3cos2θ+1Dg√3sin2θ+1
A2gsinθB2gcosθCg√3cos2θ+1Dg√3sin2θ+1 - Question 2 - Select One
In a simple pendulum, the breaking strength of the string is double the weight of the bob. The bob is released from rest when the string is horizontal. The string breaks when it makes an angle θ with the vertical.
Aθ=cos−1(1/3)Bθ=60∘Cθ=cos−1(2/3)Dθ=0 - Question 3 - Select One
A bob of mass m attached with a string of length l tied to a point on ceiling is released from a position when its string is horizontal. At the bottom most point of its motion, an identical mass m gently stuck to it. Find the maximum angle from the vertical to which it rotates.
A(a) cos−1(23)B(b) cos−1(34)C(c) cos−1(14)D(d) 60∘
A simple pendulum consists of a ball of mass m connected to a string of length L. The ball is pulled aside so that the string makes an angle of 53∘ with the verticle and is released. Find the ratio of the minumum and the tension in the string.
View SolutionA small ball of mass m is attached to a piece of light and released from rest at an angle ϕ0=37∘ from the verticle as shown which of the graphs best represents the tension in the string as a function of the angle ϕ (also relative to the vertical)?
 View Solution
View SolutionA mass is attached to the end of a string of length l which is tied to a fixed point O. The mass is released from the initial horizontal position of the string. Below the point O at what minimum distance a peg P should be fixed so that the mass turns about P and can describe a complete circle in the vertical plane?
View SolutionIn the figure, blocks A and B of masses 2m and m are connected with a string and system is hanged vertically wioth the help of spring. Spring has negligible mass. Find out magnitude of acceleration of masses 2 m and m just after the instant when the string is cut
View SolutionA pendulum is made by attaching a ball at the end of a string (the other end of the string is attached to the ceiling). The ball is released from rest at the position shown at some angle ϕ. Which of the following vectors may represent the impulse delivered by the string to the ball from the time it is released unitl the ball is at the bottom of the swing when string becomes vertical
 View Solution
View Solution
