A simple pendulum of length I and mass (bob) m is suspended vertically. The string makes an angle θ with the vertical. The restoring force acting on the pendulum is
mv2/L
mg.cosθ+mv2/L
mg.cosθ−mv2/L
mg.cosθ
The correct Answer is:B
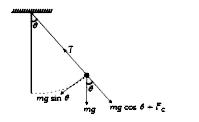
From the figure T=mgcosθ+mv2/L
Topper's Solved these Questions
- MOTION IN TWO DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - NCERT BASED QUESTIONS (HORIZONTAL PROJECTILE MOTION)
11 Videos
- MOTION IN TWO DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - NCERT BASED QUESTIONS (OBLIQUE PROJECTILE MOTION)
47 Videos
- MOTION IN TWO DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - ASSERTION & REASON
19 Videos
- MOTION IN ONE DIMENSIONBOOK - ERRORLESSCHAPTER - MOTION IN ONE DIMENSIONEXERCISE - ASSERTION AND REASON
24 Videos
- NEWTON'S LAWS OF MOTIONBOOK - ERRORLESSCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - ASSERTION & REASON
18 Videos
Similar Questions
A nail is located at a certain distance vertically below the point of suspension of a simple pendulum. The pendulum bob is released from a position where the string makes an angle of 60∘ with the vertical. Calculate the distance of nail from the point of suspension such that the bob will just perform revolutions with the nail as centre. Assume the length of the pendulum to be one meter.
View SolutionA simple pendulum of length l and with a bob of mass m moving alon a circular are of angle θ in a vertical plane. A sphere of mass m is placed at the end of the circular arc. What momentum will be given to the sphere by the moving bob?
View Solution
Knowledge Check
A simple pendulum of length l and mass (bob) m is suspended vertically. The string makes an angle θ with the vertical. The restoring force acting on the pendulum is
AmgtanθB−mgsinθCmgsinθD−mgcosθA simple pendulum of length L swings in a vertical plane. The tension of the string when it makes an angle θ with the vertical and the bob of mass m moves with a speed v is (g is the gravitational acceleration)
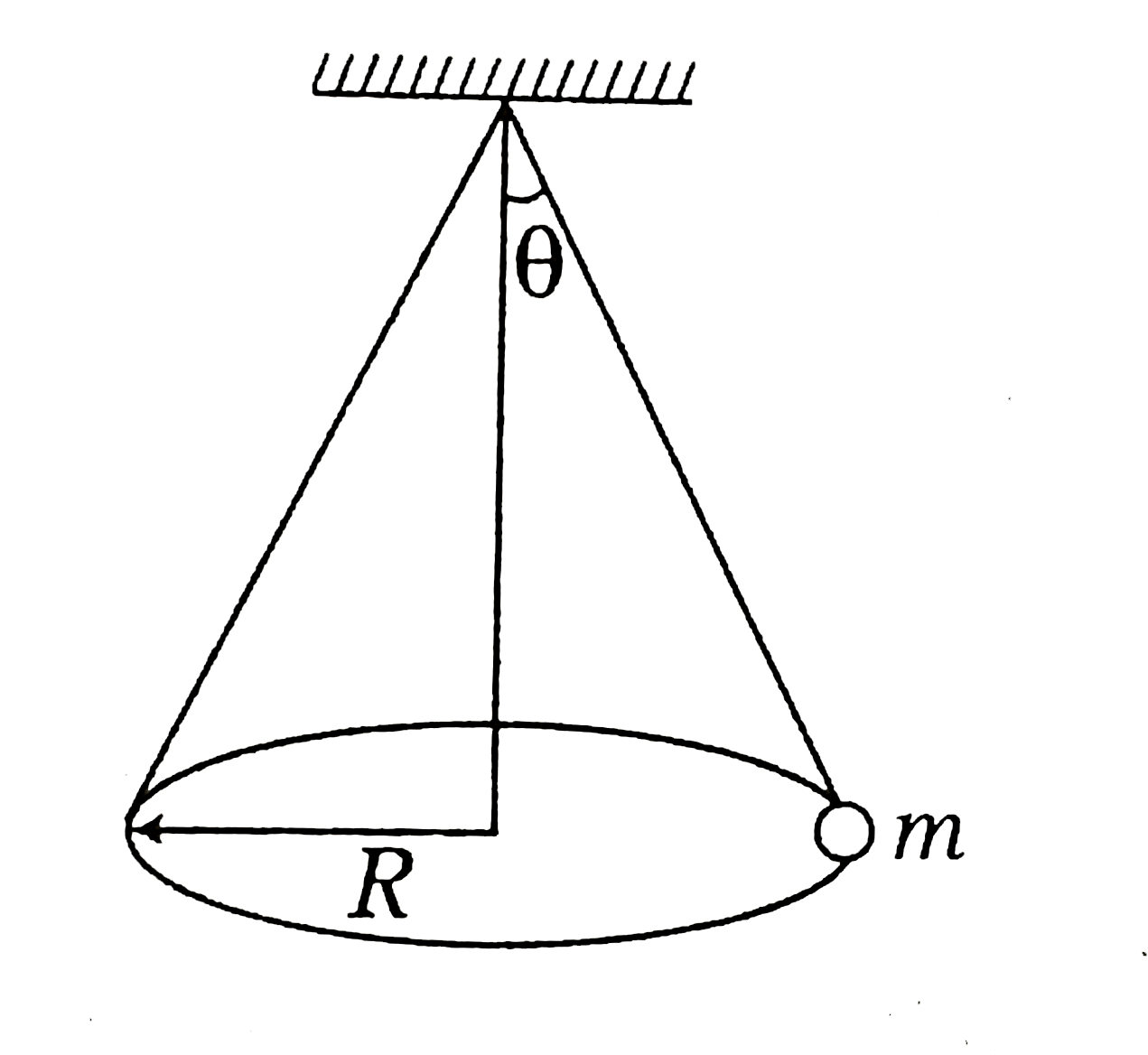
Amv2/LBmgcosθ+mv2/LCmgcosθ−mv2/LDmgcosθA conical pendulum of length L makes an angle θ with the vertical. The time period will be
 A2π√lcosθgB2π√LgcosθC2π√LtanθγD2π√Lgtanθ
A2π√lcosθgB2π√LgcosθC2π√LtanθγD2π√Lgtanθ
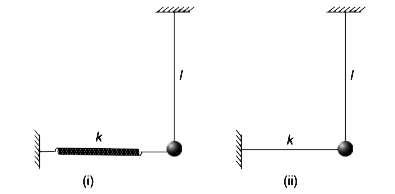
A simple pendulum of length L has a bob of mass m. The bob is connected to light horizontal spring of force constant k. The spring is relaxed when the pendulum is vertical (see fig (i)).
(a) The bob is pulled slightly and released. Find the time period of small oscillations. Assume that the spring remains horizontal.
(b) The spring is replaced with an elastic cord of force constant k. The cord is relaxed when the pendulum is vertical (see fig (ii)). The bob is pulled slightly and released. Find the time period of oscillations.
View SolutionA simple pendulum is released from rest at the horizontally stretched position. When the string makes an angle θ with the vertical, the angle θ which the acceleration vector of the bob makes with the string is given by–

View SolutionA nail is fixed at a point P vertically below the point of suspension 'O' of simple pendulum of length 1m. The bob is released when the string of pendulum makes an angle 30∘ with horiozontal. The bob reaches lowest point and then describes vertical circle whose centre coincides with P . The least distance of P from O is
View SolutionA heavy small sized sphere is suspended by a string of length 2. The sphere is rotated uniformly in a horizontal circle with the string making an angle θwith the vertical. The time period of this conical pendulum is
View SolutionA heavy small sized sphere is suspended by a string of length l . The sphere rotates uniformly in a horizontal circle with the string making an angle θ with the vertical. Then the time period of this conical pendulum is-
View Solution
