A balloon is moving with the wind in a horizontal line at a height of m. The angle of elevation of the balloon from a point A on the ground is . After some time, the angle of elevation changes to . Find the distance travelled by the balloon.
72 m
78 m
86 m
82 m
The correct Answer is:A
To solve the problem step by step, we will use trigonometric relationships in right triangles formed by the balloon's height and the angles of elevation.
Step 1: Understand the Problem
We have a balloon at a height of 36√3 meters. The angle of elevation from point A to the balloon is initially 60∘ and later changes to 30∘. We need to find the horizontal distance travelled by the balloon.
Step 2: Draw the Diagram
Draw a horizontal line representing the ground. Mark point A on this line. Draw a vertical line from point A to represent the height of the balloon, which is 36√3 m. Mark the position of the balloon at two different points corresponding to the angles of elevation 60∘ and 30∘.
Step 3: Set Up the Right Triangles
From point A, draw lines to the balloon at the two angles of elevation:
- For 60∘, label the point where the balloon is as point B.
- For 30∘, label the new position of the balloon as point C.
Step 4: Calculate the Distances
Using the tangent function, we can find the horizontal distances from point A to points B and C.
1. For angle 60∘:
tan(60∘)=HeightDistance AB⇒√3=36√3d1
Solving for d1:
d1=36√3√3=36 meters
2. For angle 30∘:
tan(30∘)=HeightDistance AC⇒1√3=36√3d2
Solving for d2:
d2=36√3⋅√3=36⋅3=108 meters
Step 5: Calculate the Distance Travelled by the Balloon
The distance travelled by the balloon is the difference between the two distances:
Distance travelled=d2−d1=108−36=72 meters
Final Answer
The distance travelled by the balloon is 72 meters.
---
We have a balloon at a height of 36√3 meters. The angle of elevation from point A to the balloon is initially 60∘ and later changes to 30∘. We need to find the horizontal distance travelled by the balloon.
Draw a horizontal line representing the ground. Mark point A on this line. Draw a vertical line from point A to represent the height of the balloon, which is 36√3 m. Mark the position of the balloon at two different points corresponding to the angles of elevation 60∘ and 30∘.
From point A, draw lines to the balloon at the two angles of elevation:
- For 60∘, label the point where the balloon is as point B.
- For 30∘, label the new position of the balloon as point C.
Using the tangent function, we can find the horizontal distances from point A to points B and C.
tan(60∘)=HeightDistance AB⇒√3=36√3d1
Solving for d1:
d1=36√3√3=36 meters
tan(30∘)=HeightDistance AC⇒1√3=36√3d2
Solving for d2:
d2=36√3⋅√3=36⋅3=108 meters
The distance travelled by the balloon is the difference between the two distances:
Distance travelled=d2−d1=108−36=72 meters
The distance travelled by the balloon is 72 meters.
Topper's Solved these Questions
- IMO QUESTION PAPER 2019 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2019 SET BEXERCISE - EVERYDAY MATHEMATICS
10 Videos
- IMO QUESTION PAPER 2019 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2019 SET BEXERCISE - ACHIEVERS SECTION
5 Videos
- IMO QUESTION PAPER 2019 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2019 SET AEXERCISE - Achievers section
5 Videos
- IMO QUESTION PAPER 2020 SET 1BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 1EXERCISE - Achievers Section
5 Videos
Similar Questions
A 1.2m tall girl spots a balloon moving with the wind in a horizontal line at a height 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°.After sometime, the angle of elevation reduces 30°.Find the distance travelled by the balloon during the interval.
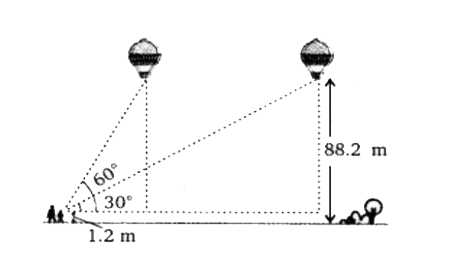
View SolutionA 1.2 m tall girl spots a ballon moving with the wind in a horizontal line at a height of 88.2 m from a ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 600. After some time, the angle of elevation reduces to 300. Find the distance travelled by the balloon during the interval.
View Solution
Knowledge Check
The angle of elevation of an object on a hill from a point on the ground is 30∘. After walking 120 metres the elevation of the object is 60∘. The height of the hill is
A120 mB60√3 mC120√3 mD60 mThe angle of elevation of the top of a tower at a point on the ground is 30∘. If on walking 20 m toward the tower, the angle of elevation becomes 60∘, then the height of the tower is
A10 mB10√3mC10√3mDNone of theseThe angle of elevation of an aeroplane from a point on the ground is 60∘ .After 15 seconds flight ,the elevation changes to 30∘ .If the aeroplane is flying at a height of 1500√3 m , find the speed of the plane
A300 m / secB200 m /secC100 m /secD150 m/sec
A 1.2 m tall girl spots a ballon moving with wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60∘. After some time, the angle of elevation reduces to 30∘. Find the distance travelled by the balloon during the interval.
View SolutionA boy whose eye level is 1.3m from the ground, spots a balloon moving with the wind in a horizontal line at same height from the ground. The angle of elevation of the balloon from the eyes of the boy at an instant is 60∘. After 2 seconds, the angle of elevation reduces to 30∘. If the speed of the wind is 29√3m/s then find the height of the balloon from the ground.
View SolutionThe angle of elevation of the top of a tower from a point on the ground is 30∘. After walking 45 m towards the tower, the angle of elevation becomes 45∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground is 30∘. After walking 40√3 m towards the tower, the angle of elevation becomes 60∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 30°. Find the height of the tower.
View Solution
