In the given figure, AX and BY are line segments such that AX || BY. Which of the following options is correct?
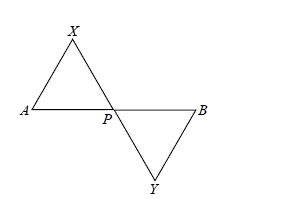
ΔAPX≅ΔPBY
AP=PB
ΔPAX≅ΔYPB
AX=XP
The correct Answer is:B
Step by step video, text & image solution for In the given figure, AX and BY are line segments such that AX || BY. Which of the following options is correct? by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- IMO QUESTION PAPER 2020 SET 1BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 1EXERCISE - Everyday Mathematics
10 Videos
- IMO QUESTION PAPER 2020 SET 1BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 1EXERCISE - Achievers Section
5 Videos
- IMO QUESTION PAPER 2018 SET B BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2018 SET B EXERCISE - Achievers Section
5 Videos
- IMO QUESTION PAPER 2020 SET 2BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 2EXERCISE - Achievers Section
5 Videos
Similar Questions
Knowledge Check
Which of the following options is correct for the given figures ?
 A X YHomogamyIsogamyB X YAnisogamyIsogamyC X YHeterogamyAnisogamyD X YIsogamyOogamy
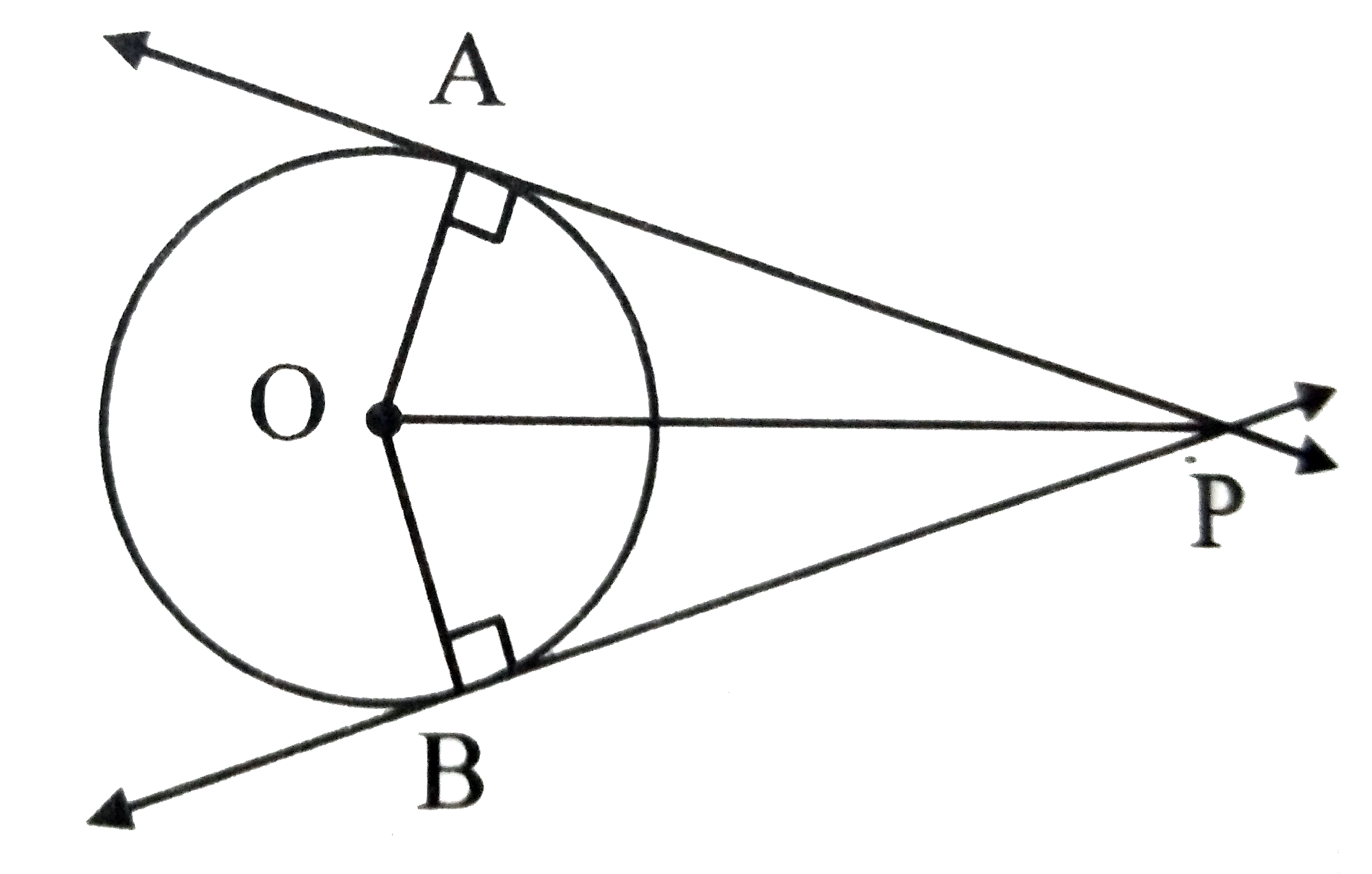
A X YHomogamyIsogamyB X YAnisogamyIsogamyC X YHeterogamyAnisogamyD X YIsogamyOogamyIn the given figure, if ∠APO=35∘, then which of the following options is correct?
 A∠BPO=35B∠BPO=55∘C∠APB=80∘D∠APB=60∘
A∠BPO=35B∠BPO=55∘C∠APB=80∘D∠APB=60∘If all bond angles in AX3 molecule are the same, then which of the following conclusions is correct about AX3?
AAX3 must be polar.BAX3 must be planar.CAX3 must have at least 5 valence electrons.DX must connect from central atom with either single bond or double bond.
For the figure given below, which of the following options is correct?
View SolutionConsider the given figure.

Which of the following option is correct for the labels A to C ?
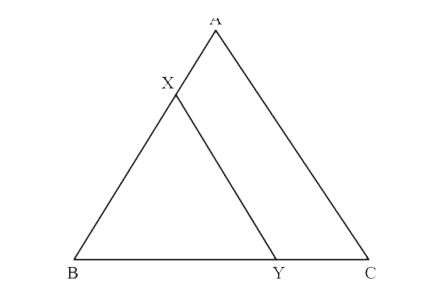
View SolutionIn the given figure, the line segment XY is Parallel to AC of ΔABC and it divides the triangle into two parts of equal areas. Prove that AXAB=√2−1√2
View Solutionfor the given figure, choose the correct option
View SolutionIn Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
View Solution


