Choose the correct expression of energy stored in an inductor ?
U=1/2LI20
U=1/2LI0
U=1/3LI30
None of the above
The correct Answer is:A
To find the correct expression for the energy stored in an inductor, we can follow these steps:
1. Understanding the Concept: The energy stored in an inductor is related to the work done to establish the current through it. When current flows through an inductor, it creates a magnetic field, and energy is stored in that magnetic field.
2. Formula for Energy in an Inductor: The energy (U) stored in an inductor can be derived from the work done to establish the current. The formula for the energy stored in an inductor is given by:
U=12LI2
where:
- U = energy stored in the inductor,
- L = inductance of the inductor,
- I = current flowing through the inductor.
3. Identifying the Variables: In the expression, I can be represented as I0 (the maximum or steady-state current), so we can rewrite the formula as:
U=12LI20
4. Evaluating the Options: Now, let's evaluate the given options:
- Option 1: U=12LI20 (This matches our derived formula)
- Option 2: U=12LI0 (This is incorrect)
- Option 3: U=13LI30 (This is incorrect)
- Option 4: None of the above (This is incorrect since we have a correct option)
5. Conclusion: The correct expression for the energy stored in an inductor is:
U=12LI20
Thus, the correct answer is Option 1.
U=12LI2
where:
- U = energy stored in the inductor,
- L = inductance of the inductor,
- I = current flowing through the inductor.
U=12LI20
- Option 1: U=12LI20 (This matches our derived formula)
- Option 2: U=12LI0 (This is incorrect)
- Option 3: U=13LI30 (This is incorrect)
- Option 4: None of the above (This is incorrect since we have a correct option)
U=12LI20
Thus, the correct answer is Option 1.
Similar Questions
Define self-inductance of a coil. Obtain the expression for the energy stored in an inductor L connected across a source of emf.
View SolutionDefine the term self indutance of a solenoid. Obtained the expresssion for the magnetic energy stored in an inductor or self-inductance L to a build up a certain I through it.
View SolutionIn the steady state of the circuit shown in the figure the ratio of energy stored in the inductor to th energy stored in the capacitor is 1000000.
 View Solution
View SolutionChoose the option with correct expression.
View SolutionChoose the correct Boolean expression for the given circuit diagram:
 View Solution
View SolutionThe energy stored in 4μF capacitors is
View SolutionObtain the expression for the magnetic energy stored in an ideal inductor of self inductance L when a current I passes through it.
Hence obtain the expression for the energy density of magentic field produced in the inductor.View SolutionThe cell in the circuit shows in Fig is ideal. The coil has an inductance of 4mH and a resistance of 2mΩ. The switch is closed at t=0. The amount of energy stored in the inductor at t=2s is (take e=3)
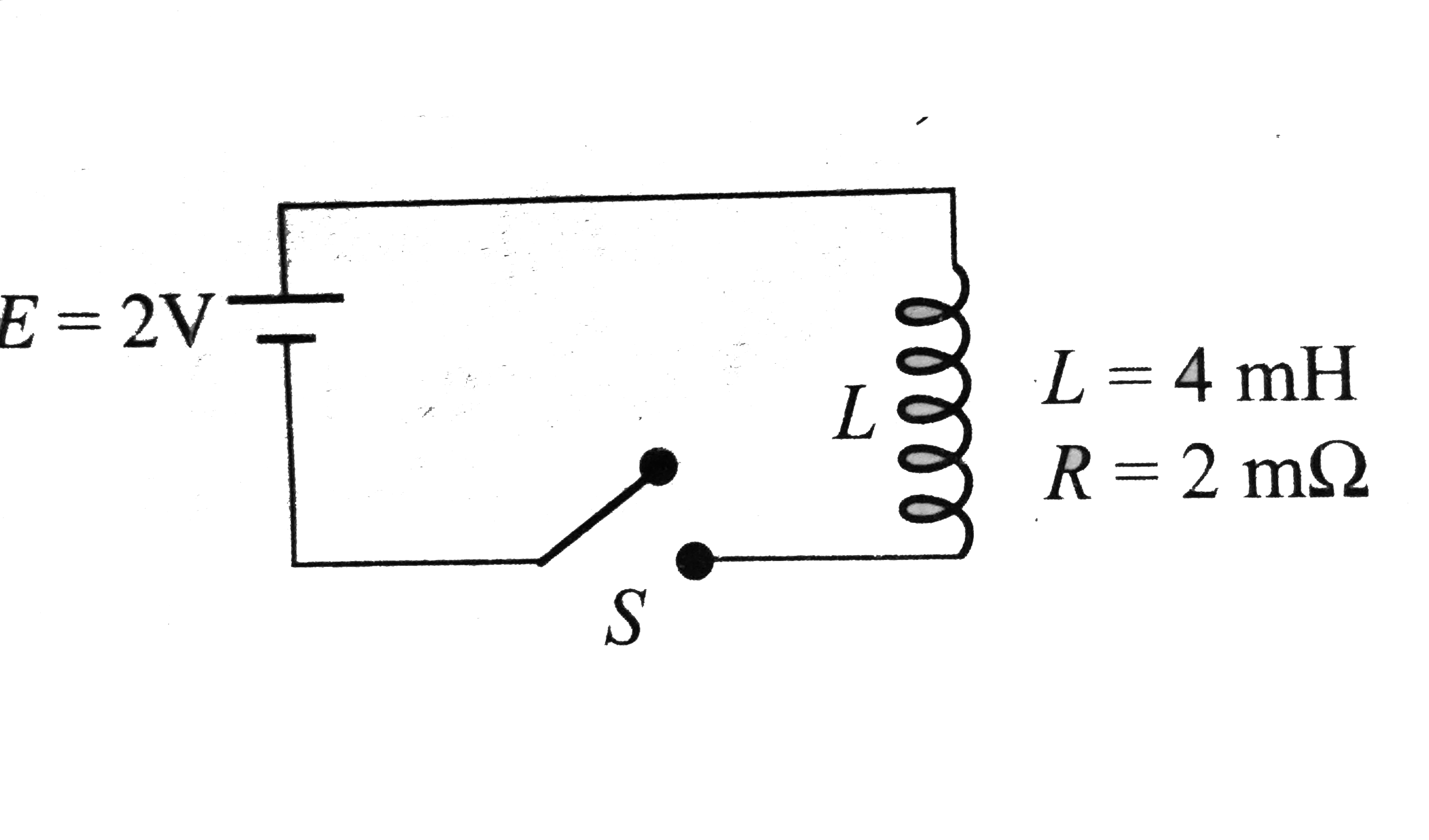 View Solution
View SolutionConsider the RL circuit in Fig. When the switch is closed in position 1 and opens in position 2, electrical work must be performed on the inductor and on the resistor. The energy stored in the inductor is for the resistor energy appears as heat.
a. What is the ratio of PL/PR of the rate at which energy is stored in the inductor to the rate at which energy is dissipated in the resistor?
b. Express the ratio PL/PR as a function of time.
c. If the time constant of circuit is t, what is the time at which PL=PR?View SolutionAn L−C circuit consists of an inductor with L=0.0900H and a capacitor of C=4x10−4F. The initial charge on the capacitor is 5.00μC, and the initial current in the inductor is zero.
(a) What is the maximum voltage across the capacitor?
(b) What is the maximum current in the inductor?
(c) What is the maximum energy stored in the inductor?
(d) When the current in the inductor has half its maximum value, what is the charge on the capacitor and what is the energy stored in the inductor?View Solution

