When a charged particle is projected perpendicular to a uniform magnetic field, it describes a circular path in which :
its speed remains constant.
its velocity remains constant.
its momentum remains constant.
its kinetic energy increases.
The correct Answer is:A
when particle is projected perpen dicular to a uniform magnetic field its velocity changes but speed remains constant.
Similar Questions
A charged particle is projected perpendicular to uniform magnetic field. It describes a circle, the quantities which are inversely proportional to specific charge are
i) Radius ii) K. E
iii) Time period iv) Momentum
View SolutionIf a charged particle enters perpendicular in the uniform magnetic field then
View SolutionIf a charged particle is a plane perpendicular to a uniform magnetic field with a time period T Then
View SolutionStatement-1 A charged particle when projected perpendiculary to a uniform magnetic field, its velocity is constant through out its motion
Statement-2 A charged particle its acceleration is zero
Statement-3 A charged particle when projected perpendicular to a uniform magnetic field, a magnetic force acts on it but that does not change particle's speed
View SolutionThe path of a charged particle projected into a uniform transverse electric field is
View SolutionAssertion When a charged particle moves perpendicular to a uniform magnetic field then its momentum remains constant.
Reason Magnetic force acts perpendicular to the velocity of the particle.
View SolutionParticles 1, 2 and 3 are moving perpendicular to a uniform magnetic field, then particle
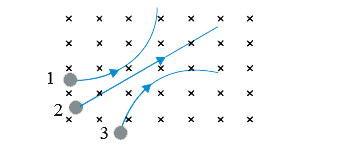
View SolutionWhen would a moving charged particle travel undeviated in a uniform magnetic field ?
View SolutionMagnetic force acting on the charged particle projected perpendicular to magnetic field is proportional to rn, where r is radius of circular path. Find n
View SolutionA charged particle (q,m) enters perpendicular in a uniform magnetic field B and comes out field as shown. Find the angle of deviation θ for particle to cross magnetic field will be
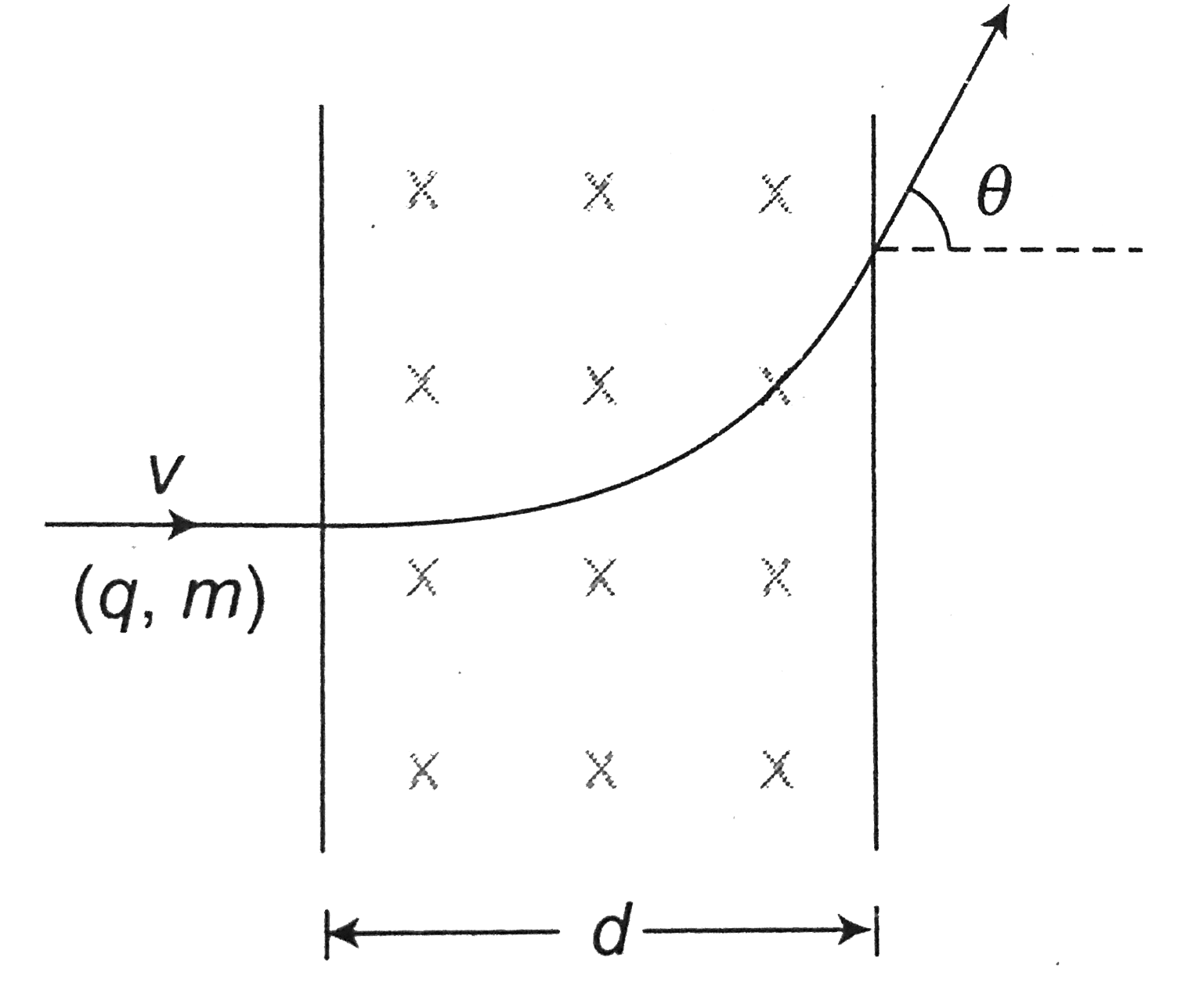
View Solution
