The corner points of the feasible region determined by the system of linear constraints are (0,10),(5,5),(15,15),(0,20). Let Z=px+qy, where . Condition on p and q so that the maximum of Z occurs at both the points (15,15) and (0,20) is:
p=q
p=2q
q=2p
q=3p
The correct Answer is:D
To solve the problem, we need to find the conditions on p and q such that the maximum value of Z=px+qy occurs at both points (15,15) and (0,20).
1. Define the Objective Function:
The objective function is given by:
Z=px+qy
2. Calculate Z at the Point (15,15):
Substitute x=15 and y=15 into the objective function:
Z(15,15)=p(15)+q(15)=15p+15q
3. Calculate Z at the Point (0,20):
Substitute x=0 and y=20 into the objective function:
Z(0,20)=p(0)+q(20)=20q
4. Set the Two Expressions for Z Equal:
Since we want the maximum value of Z to occur at both points, we set the two expressions equal to each other:
15p+15q=20q
5. Rearrange the Equation:
Rearranging gives:
15p+15q−20q=0⟹15p−5q=0
6. Solve for q in Terms of p:
From the equation 15p−5q=0, we can express q in terms of p:
15p=5q⟹q=3p
Conclusion:
The condition on p and q such that the maximum of Z occurs at both points (15,15) and (0,20) is:
q=3p
The objective function is given by:
Z=px+qy
Substitute x=15 and y=15 into the objective function:
Z(15,15)=p(15)+q(15)=15p+15q
Substitute x=0 and y=20 into the objective function:
Z(0,20)=p(0)+q(20)=20q
Since we want the maximum value of Z to occur at both points, we set the two expressions equal to each other:
15p+15q=20q
Rearranging gives:
15p+15q−20q=0⟹15p−5q=0
From the equation 15p−5q=0, we can express q in terms of p:
15p=5q⟹q=3p
The condition on p and q such that the maximum of Z occurs at both points (15,15) and (0,20) is:
q=3p
Similar Questions
The corner points of the feasible region determined by the following system of linear inequalities:
2x+y≥10,x+3y≤15,x,y≥0 are (0,0),(5,0),(3,4) and (0,5). Let Z=px+qy, where p,q≥0. Condition on p and q so that the maximum of Z occurs at both (3,4) and (0,5) is:
(a) p=q (b) p=2q (c) p=eq (d) q=3p
View SolutionFor an objective function Z=ax+by, where a,b>0, the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20), (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum Z occurs at both the points (30, 30) and (0, 40) is:
View Solution
Knowledge Check
The corner points of the feasible region determined by the system of linear constraints are (0,10) , (5,5) (25,20),(0,30) Let z = px + qy , where p,q>0 Condition on p and q so that te maximum of z occurs at both the points (25,20 ) and (0,30) is ………
A5p = 2qB2p=5qCp = 2qDq = 3pThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q>0. Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
Ap=qBp=2qCq=2pDq=3pCorner points of the feasible region determined by the system of linear constraints are (0,3), (1,1), and (3,0). Let Z=px+qy. Where p,q<0 Condition on p and q, so that the minimum of Z occurs at (3,0) and (1,1) is
Ap=2qBp=q2Cp=3qDp=q
The corner points of the feasible region determined by the system of linear constraints are as shown below:
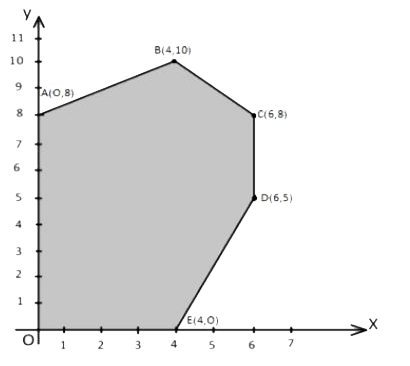
Let Z=px+qy where p,q>0 be the objective function. Find the condition on p and q so that the maximum value of Z occurs atB(4,10)andC(6,8)Also mention the number of optimal solutions in this case.
View SolutionThe corner points of a feasible region determined by a system of linear inequations are (0,0),(4,0),(5,2),(2,2) and (0, 1). If the objective function is Z = x + y, then maximum of Z occurs at:
View SolutionThe corneer points of a feasible region, determined by a system of linear inequations, are (0,0),(1,0),(4,3),(2,1)and(0,1). If the objective function is Z=2x−3y, then the minimum value of Z is :
View SolutionFor an objective function Z = ax + by, where a,b>0, the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20). (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum z occurs at both the points (30, 30) and (0, 40) is:
View SolutionThe corner points of the feasible region determined by the system of linear contraints are (0,0), (0,40),( 20,40),(60,20),(60,0). The objective function is Z=4x+3y. Compare the quantity in Column A and Column B.
View Solution
