27 charges of equal values are combined together to make a large charge. It the potential of each charge is 5 V, then the potential of the big charge will be:
40 V
45 V
50 V
55 V
The correct Answer is:B
To solve the problem, we need to determine the potential of a large charge formed by combining 27 smaller charges, each with a potential of 5 V. Here’s a step-by-step solution:
Step 1: Understand the relationship between charge and potential
The potential V of a point charge is given by the formula:
V=kQr
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge.
Step 2: Define the charges
Let the charge of each smaller charge be Q. Since there are 27 such charges, the total charge Q′ of the larger charge will be:
Q′=27Q
Step 3: Relate the radii of the charges
When combining the charges, we assume that the smaller charges are combined into a larger spherical charge. If the radius of each smaller charge is r, then the radius of the larger charge R can be derived from the volume relationship:
Volume of smaller charge=43πr3
Volume of larger charge=43πR3
Since the total volume of the smaller charges equals the volume of the larger charge:
27(43πr3)=43πR3
Cancelling 43π from both sides gives:
27r3=R3
Taking the cube root of both sides:
R=3r
Step 4: Calculate the potential of the larger charge
The potential of the larger charge V′ can be expressed as:
V′=kQ′R=k(27Q)R
Substituting R=3r:
V′=k(27Q)3r=9⋅kQr
Step 5: Substitute the known potential
We know that the potential of each smaller charge is 5 V:
kQr=5V
Thus, substituting this into the equation for V′:
V′=9⋅5=45V
Conclusion
The potential of the larger charge formed by combining 27 smaller charges, each with a potential of 5 V, is:
45V
The potential V of a point charge is given by the formula:
V=kQr
where k is Coulomb's constant, Q is the charge, and r is the distance from the charge.
Let the charge of each smaller charge be Q. Since there are 27 such charges, the total charge Q′ of the larger charge will be:
Q′=27Q
When combining the charges, we assume that the smaller charges are combined into a larger spherical charge. If the radius of each smaller charge is r, then the radius of the larger charge R can be derived from the volume relationship:
Volume of smaller charge=43πr3
Volume of larger charge=43πR3
Since the total volume of the smaller charges equals the volume of the larger charge:
27(43πr3)=43πR3
Cancelling 43π from both sides gives:
27r3=R3
Taking the cube root of both sides:
R=3r
The potential of the larger charge V′ can be expressed as:
V′=kQ′R=k(27Q)R
Substituting R=3r:
V′=k(27Q)3r=9⋅kQr
We know that the potential of each smaller charge is 5 V:
kQr=5V
Thus, substituting this into the equation for V′:
V′=9⋅5=45V
The potential of the larger charge formed by combining 27 smaller charges, each with a potential of 5 V, is:
45V
Similar Questions
Knowledge Check
Metallic sphere of radius R is charged to potential V. Then charge q is proportional to
AVBRCboth V and RDnone of these
Equal charges are given to two spheres of different radii. The potential will
View SolutionWhen the separation between two charges is increased, the electric potential energy of the charges
View SolutionWhen the separation between two charges is increased, the electric potential energy of the charges
View SolutionWhen the separation between two charges is increase the electric potential energy of the charges.
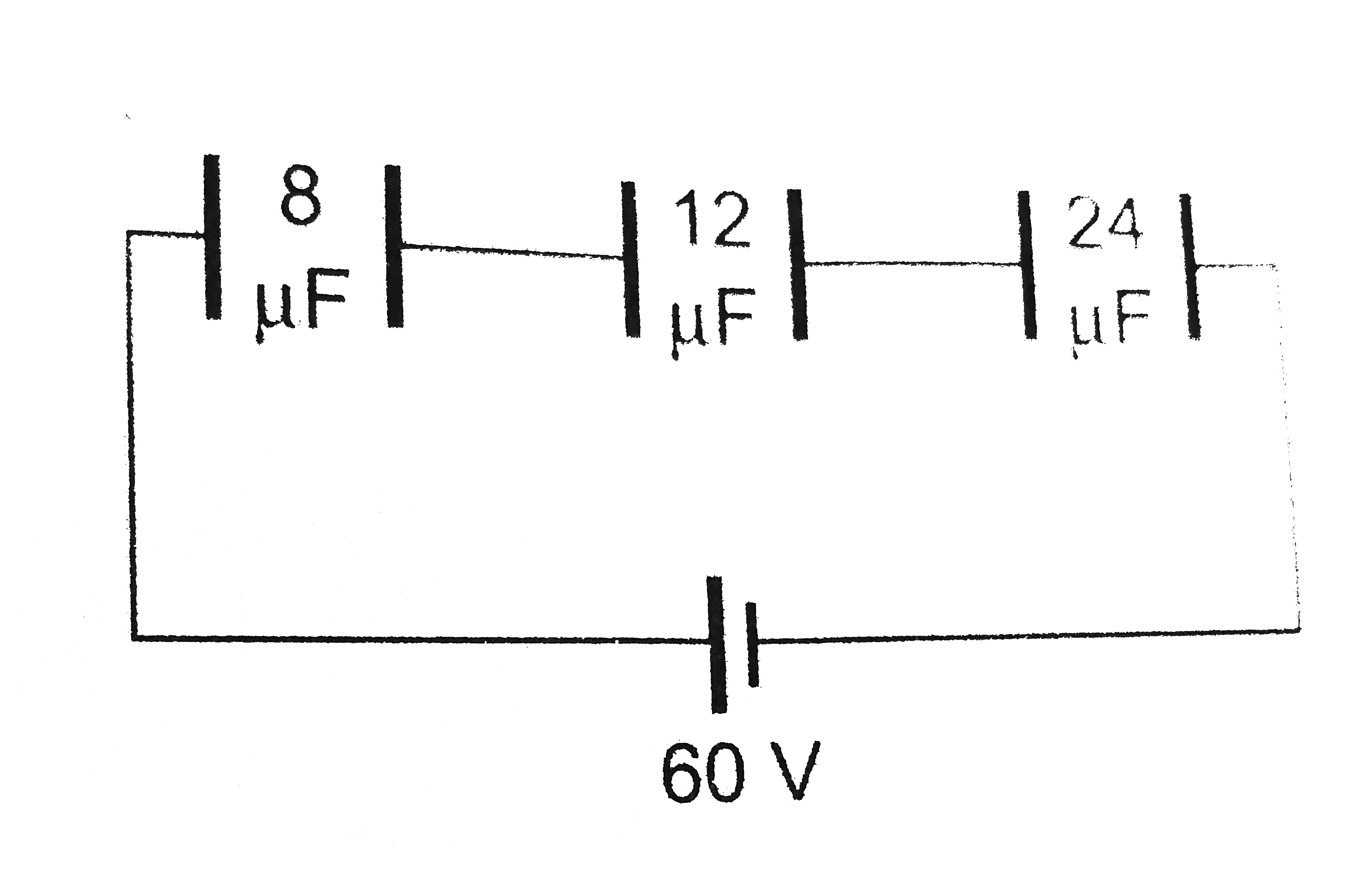
View SolutionFind the potential difference and charge on each capacitor.
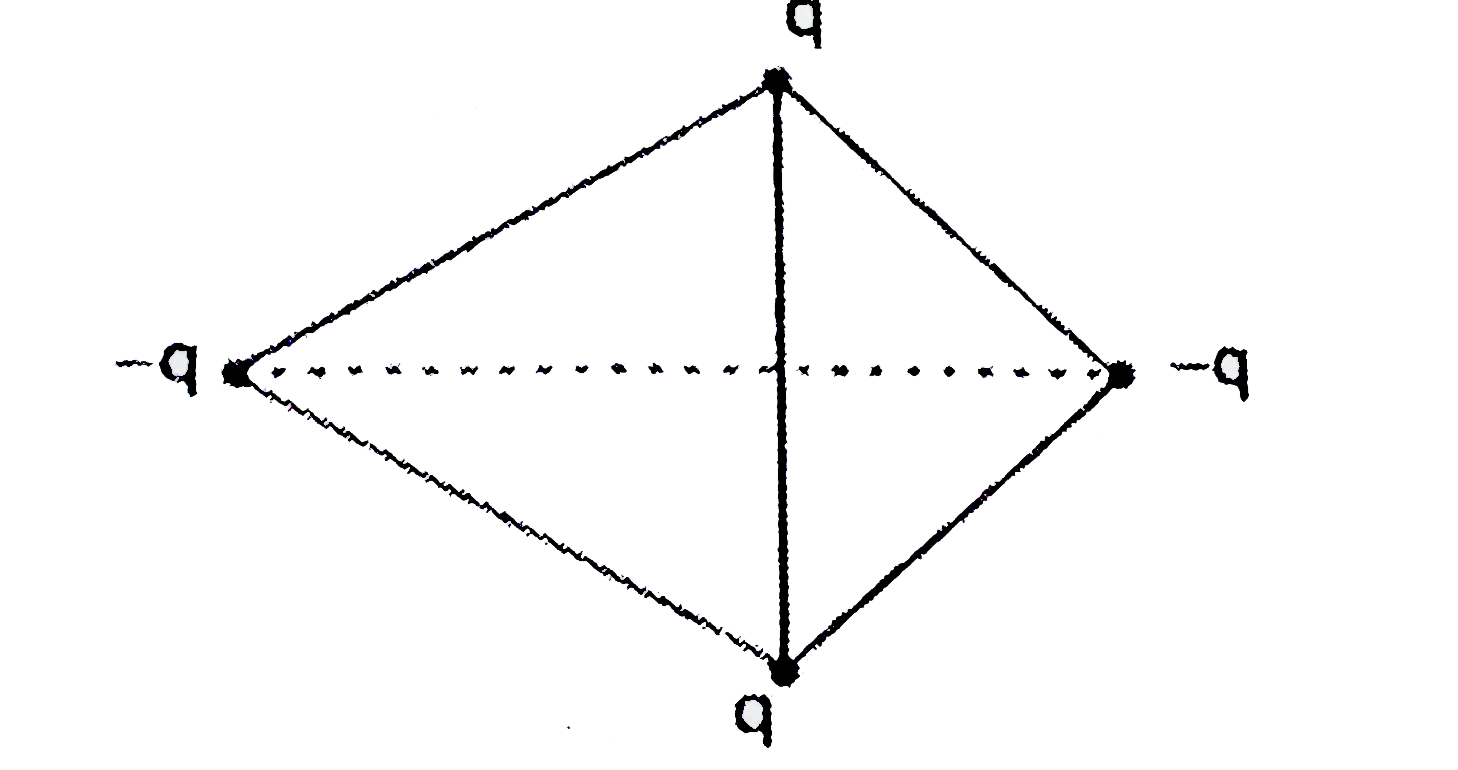
View SolutionFour small point charges (each of equal magnitude q) are placed at four corners of a regular tetrahedron of side a. find out potential energy of charge system
View SolutionA hollow metal sphere of radius 10 cm is charged such that the potential on its surface is 5 V. What is the potential at the centre of the sphere?
View Solution
