The magnetic field due to a current in a straight wire segment of length L at a point on its perpendicular bisector at a distance r(r>>L).
decreases as 1r
decreases as 1r3
decreases as 1r2
increases as r2
The correct Answer is:C
To find the magnetic field due to a current in a straight wire segment of length L at a point on its perpendicular bisector at a distance r (where r≫L), we can use the Biot-Savart Law. Here’s the step-by-step solution:
Step 1: Understand the Biot-Savart Law
The Biot-Savart Law states that the magnetic field dB at a point in space due to a small segment of current-carrying wire is given by:
dB=μ04πIdL×^rr2
where:
- μ0 is the permeability of free space,
- I is the current,
- dL is the length of the wire segment,
- ^r is the unit vector pointing from the wire segment to the point where the magnetic field is being calculated,
- r is the distance from the wire segment to the point.
Step 2: Set Up the Geometry
For a straight wire segment of length L, we consider a point on its perpendicular bisector at a distance r. The distance from the midpoint of the wire to the point where we are calculating the magnetic field is r.
Step 3: Calculate the Magnetic Field Contribution
Since the wire segment is straight and the point is on the perpendicular bisector, the contributions to the magnetic field from both ends of the wire will add up. The angle θ between dL and ^r is 90∘, so sin(θ)=1.
The total magnetic field B at the point is given by integrating dB over the length of the wire:
B=∫dB=∫μ04πIdLr2
Step 4: Evaluate the Integral
Since r is constant for the entire length of the wire segment, we can take it out of the integral:
B=μ0I4πr2∫dL
The integral ∫dL over the length L gives us L:
B=μ0IL4πr2
Step 5: Analyze the Result
From the equation B=μ0IL4πr2, we can see that the magnetic field B is inversely proportional to the square of the distance r.
Conclusion
Thus, the magnetic field due to a current in a straight wire segment of length L at a point on its perpendicular bisector at a distance r decreases as 1r2.
The Biot-Savart Law states that the magnetic field dB at a point in space due to a small segment of current-carrying wire is given by:
- μ0 is the permeability of free space,
- I is the current,
- dL is the length of the wire segment,
- ^r is the unit vector pointing from the wire segment to the point where the magnetic field is being calculated,
- r is the distance from the wire segment to the point.
For a straight wire segment of length L, we consider a point on its perpendicular bisector at a distance r. The distance from the midpoint of the wire to the point where we are calculating the magnetic field is r.
Since the wire segment is straight and the point is on the perpendicular bisector, the contributions to the magnetic field from both ends of the wire will add up. The angle θ between dL and ^r is 90∘, so sin(θ)=1.
Since r is constant for the entire length of the wire segment, we can take it out of the integral:
From the equation B=μ0IL4πr2, we can see that the magnetic field B is inversely proportional to the square of the distance r.
Thus, the magnetic field due to a current in a straight wire segment of length L at a point on its perpendicular bisector at a distance r decreases as 1r2.
Similar Questions
The magnetic field at the origin due to the current flowing in the wire is

View SolutionThe magnetic field at the origin due to the current flowing in the wire is

View SolutionThe magnetic field in a straight current carrying conductor wire is:
View SolutionConsider a straight piece of length x of a wire carrying a current i. Let P be a point on the perpendicular bisector of the piece, situated at a distance d from its middle point. Show that for d>>x, the magnetic field at P varies as (1/d^2) whereas for d << x, it varies as 1/d.
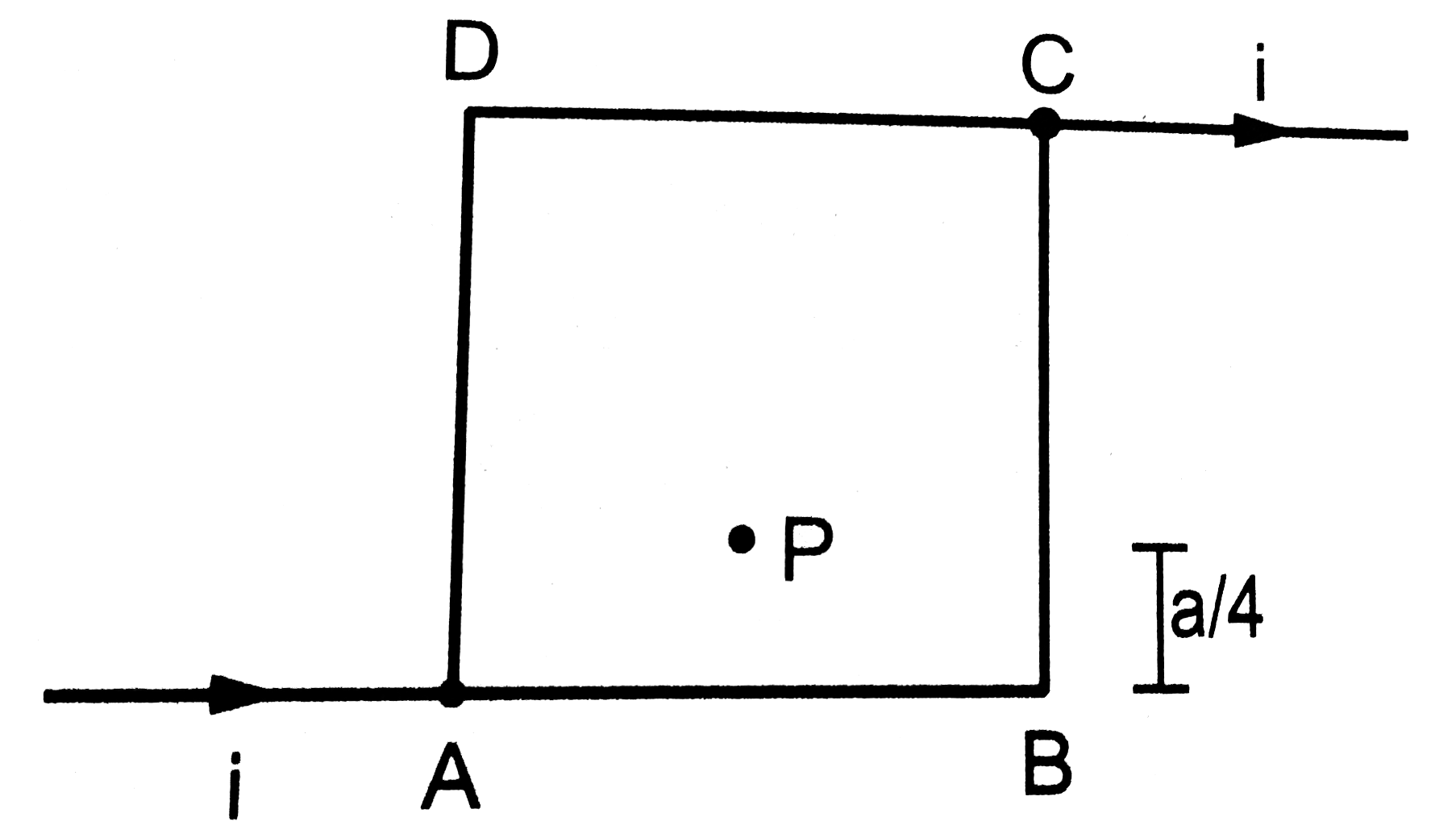
View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
View SolutionMagnetic field at point O due to straight conductor PQ is
_PHY_E06_180_Q01.png)
View SolutionFind the magnetic field at point P due to a straight line segment AB of length 6cm carrying a current of 5A. (See figure)
(μ0=4π×10−7N−A−2).
 .
.
View SolutionThe field due to a magnet at a distance R~ from the centre of the magnet is proportional
View SolutionThe moment of inertia of a uniform cylinder of length landradiusR about its perpendicular bisector is I. What is the ratio l/R such that the moment of inertia is minimum ?
View SolutionThe magnetic field ¯¯¯¯¯dB due to a small current element ¯¯¯dl at a distance →r and carrying current 'I' is
View Solution
