If the radius of circle is 7 cm, then find the perimeter of a quadrant.
25 cm
24 cm
26 cm
27 cm
The correct Answer is:A
To find the perimeter of a quadrant of a circle with a radius of 7 cm, we can follow these steps:
1. Understand the Quadrant: A quadrant is one-fourth of a circle. The perimeter of a quadrant consists of two parts: the curved part (which is one-fourth of the circumference of the circle) and the two straight sides (which are the radii of the circle).
2. Calculate the Circumference of the Circle:
The formula for the circumference C of a circle is given by:
C=2πr
where r is the radius. Here, r=7 cm.
C=2×π×7
3. Substitute the Value of π:
We can use π≈227 for our calculations.
C=2×227×7
4. Simplify the Circumference:
C=2×22=44 cm
5. Calculate the Curved Length of the Quadrant:
Since a quadrant is one-fourth of the circle, the curved length L of the quadrant is:
L=14×C=14×44=11 cm
6. Calculate the Length of the Straight Sides:
The straight sides of the quadrant are the two radii of the circle. Each radius is 7 cm, so the total length of the straight sides is:
Total straight sides=2×r=2×7=14 cm
7. Calculate the Total Perimeter of the Quadrant:
Now, we can find the total perimeter P of the quadrant by adding the curved length and the lengths of the straight sides:
P=L+Total straight sides=11+14=25 cm
Final Answer:
The perimeter of the quadrant is 25 cm.
---
The formula for the circumference C of a circle is given by:
C=2πr
where r is the radius. Here, r=7 cm.
C=2×π×7
We can use π≈227 for our calculations.
C=2×227×7
C=2×22=44 cm
Since a quadrant is one-fourth of the circle, the curved length L of the quadrant is:
L=14×C=14×44=11 cm
The straight sides of the quadrant are the two radii of the circle. Each radius is 7 cm, so the total length of the straight sides is:
Total straight sides=2×r=2×7=14 cm
Now, we can find the total perimeter P of the quadrant by adding the curved length and the lengths of the straight sides:
P=L+Total straight sides=11+14=25 cm
The perimeter of the quadrant is 25 cm.
Similar Questions
Knowledge Check
- Question 1 - Select One
If radius of circle is 7 cm, then the perimeter of the figure and area shaded portion of the given figure respectively is
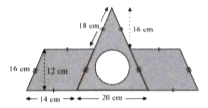 A144 cm, 462 cm2B156 cm, 462 cm2C122 cm, 294 cm2D144 cm, 394 cm2
A144 cm, 462 cm2B156 cm, 462 cm2C122 cm, 294 cm2D144 cm, 394 cm2 - Question 2 - Select One
If the radius of circle is 7 cm, then the circumference of the circle is ________.
A22 cmB44 cmC66 cmD88 cm - Question 3 - Select One
If the radius of circle is 7 cm, then the circumference of the circle is ________.
A22 cmB44 cmC66 cmD88 cm
The circumference of a circle is 220 cm. Find the perimeter of its quadrant.
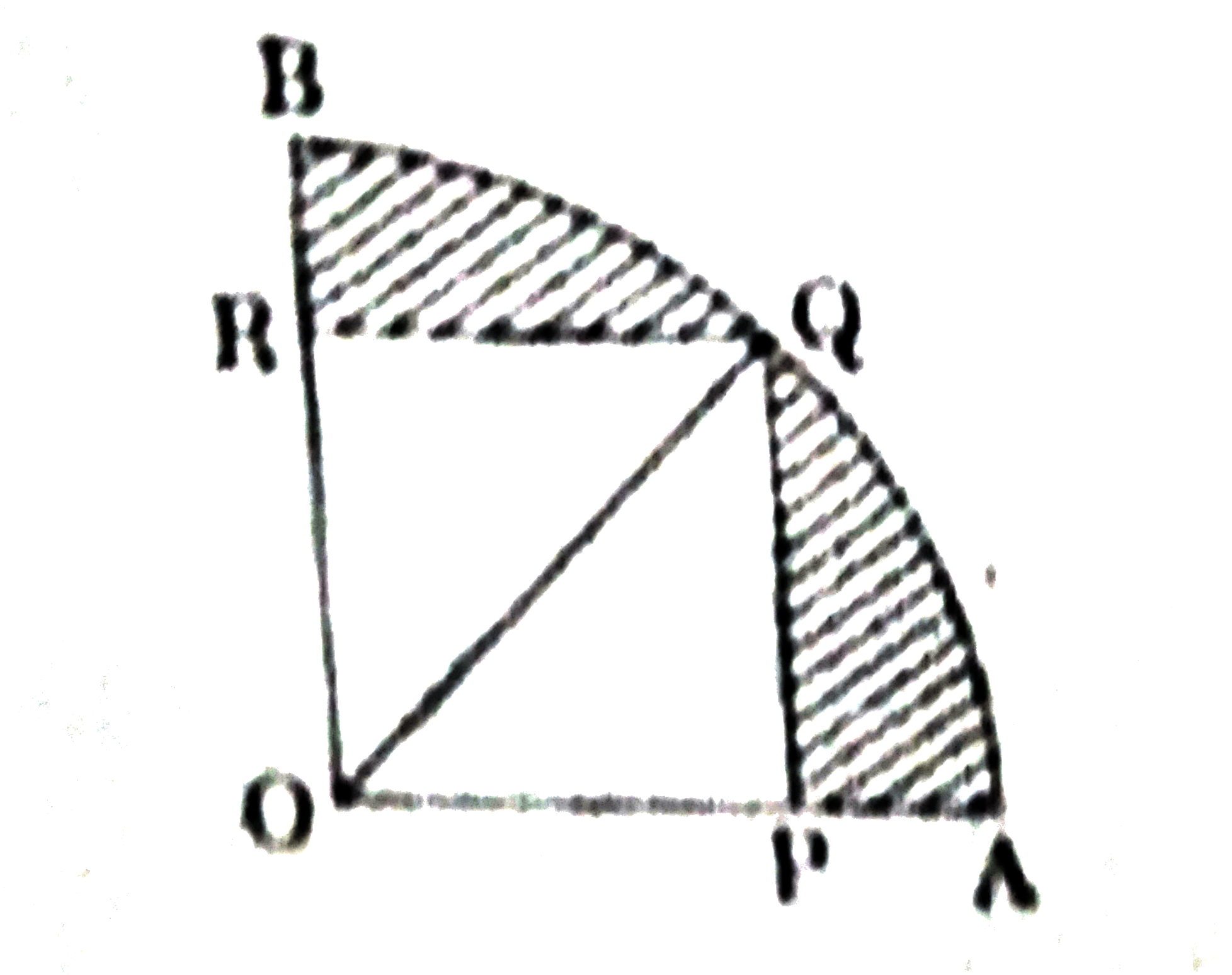
View SolutionIn Figure , a square OPQR is inscribed in a quadrant OAQB of a circle. If the radius of circle is 6√2 cm, find the area of the shaded region
 View Solution
View SolutionIn Figure-9, a square OPQR is inscribed in a quadrant OAQB of a circle. If the radius of circle is 6√2 cm, Find the area of the shaded region.
View SolutionThe radius of a circle is 4.7 cm. Find its circumference
View SolutionThe circumference of a circle is equal to the perimeter of an equilateral triangle. If the radius of the circle is 7 cm what is the length of the equilateral triangle ?
View Solution
