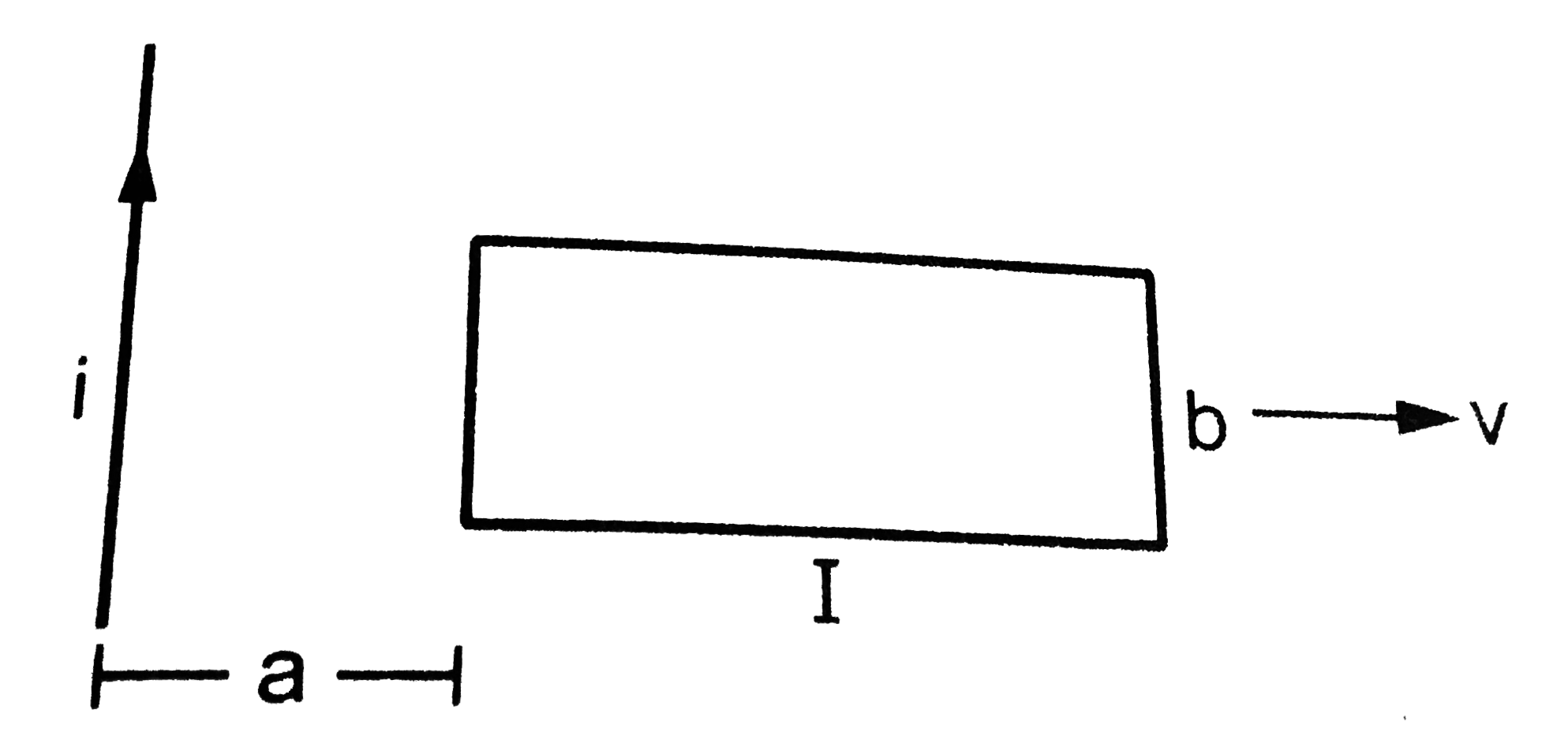
A rectangular metallic loop of length l and width b is placed coplanerly with a long wire carrying a current I . The loop is moved perpendicular to the wire with a speed v in the plane containing the wire and the loop. Calculate the emf induced in the loop when the rear end of hte loop is at a distance a from the wire. Solve by unsing Faraday's law for the flux thrugh the loop and also by replacing different sagments with equivalent batteries.
 Solution in Gujrati
Solution in Gujrati
(a) Using Faraday's law<br>Cosider a unit length dx at a distance x <br>B=(mu_0i)/(2 pi x) Area of strip =bdx<br>d phi = (mu_0i)/(2 pi x) bdx<br> implies phi= int^(a+l)_(a) (mu_0 i)/(2 pi x) bdx<br>=(mu_0 i)/(2 pi)b int_(a)^(a+l)((dx)/(x))<br>=(mu_0 i)/(2 pi x) log ((a+l)/(a))<br>Emf= (d phi)/(dt)=d/(dt)[(mu_0 i)/(2 pi) log ((a+l)/(a))]<br>=(mu_0 i)/(2 pi)((a)/(a+l)) ((va-(a+l)v)/(a^2))<br>(where (da)/(dt)=v)<br>= (mu_0ib)/(2 pi) (a)/(a+l) (vl)/(a^2)<br>=μ0ibvl2π(a+l)a
the velocities of AB and CD create e.m/f because the emf 's due to to AD and BC are equal and opposite to each other.
∴BAB=μ0i2πa
Emf_(AB)=(mu_0i)/(2 pi a)<br>length =b, velocity =v <br>B_(CD)=(mu_0i)/(2 pi(a+l))<br>Emf'_(CD)=(mu_0ibv)/(2 pi(a+l))<br>Net E.m.f.=(mu_0ibv)/(2 pi a))-(mu_0ibv)/(2 pi(a+l))<br>=(mu_0ibvl (a+l)- mu ib va)/(2 pi a(a+l))<br>(mu_0ibvl)/(2 pi(a+l)).
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises
9 Videos
Similar Questions
Shown a metallic square frame of edga a in a vertical plane. A uniform magnetic field B exists in the space in a directon perpendicular to the plane of the figure. Two boys pull the opposite corners of the square ot deform it into a rhombus. They start pulling the corners t t=0 and sisplace the corners at a uniform speed u. (a) find the induced emf in the frame at the instant when the angles at these corners reduce to 60∘. (b) find the induced current in the frame at this instatnt if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
View SolutionA bar magnet is moved along the axis of a copper ring placed far away from the magnet. Looking from the side of the magnet, an anticlockwise current is found to be induced in the ring. Which of the following may be true?
View SolutionFind the dimensional formula of ε0 .
View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
View Solutiona rectangular loop, as shown in Fig. 3.66, moves away from an infinitely long wire carrying a current I. Find the emf induced in the rectangualr loop.
View SolutionA rectangular loop is moving parallel to a long wire carrying current i with a velocity v . Find the emf induced in the loop (Fig. 3.68) if its nearest end is at a distance a from the wire. Draw equivalent electrical diagram.
View SolutionA rectangular loop of length 'l' and breadth 'b' is placed at a distance of x from an infinitely long wire carrying current 'i' such that the direction of current is parallel to breadth. If the loop moves away from the current wire in a direction perpendicular to it with a velocity 'v' , the magnitude of the e.m.f. in the loop is: ( mu_(0)= permeability of free space)
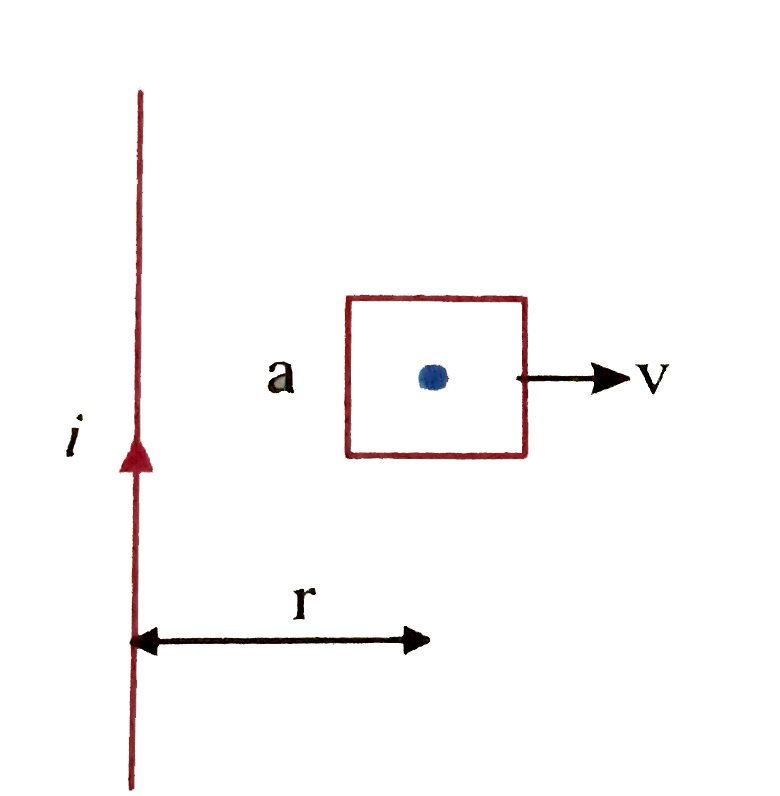
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
View SolutionA square metallic loop of side l is placed near a fixed long wire carrying a current i(figure).The loop is moved towards right perpendicular to the wire with a speed v in the plane containing the wire and the loop.The emf induced in the loop when the rear end of the loop is at a distance a=2l from the wire is μ0ivxπ.Find out value of x.

View SolutionA square meallic loop of side l is placed near a fixed long wire carrying a current i (figure). The loop is moved towards right perpendicular to the wire with a speed v in the plane containing the wire and the loop. The emf induced in the loop when the rear end of the loop is at a distance a=2l from the wire is (mu_(0)iv)/(xpi) . Find out value of x .
View SolutionA long wire carrying a steady current I lies in the plant of a circular conducting loop placed at a certain distance from the wire . There will be an induced current in the loop if it is
View SolutionA long wire carrying a steady current I lies in the plane of circular conducting loop placed at a certain distance from the wire. There will be an induced current in the loop if it is
View SolutionA square (each side of length L) wire loop is kept with a long straight wire carrying current I. The emf induced in the square loop is _____
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from the wire where r > > a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f. in the loop is
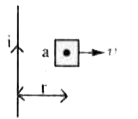
View SolutionA square loop of side a is placed in the same plane as a long straight wire carrying a current i . The centre of the loop is at a distance r from wire where r gt gt a . The loop is moved away from the wire with a constant velocity v . The induced e.m.f in the loop is
View SolutionA rectangular loop of length 'l' and breadth 'b' is placed at a distance of x from an infinitely long wire carrying current 'i' such that the direction of current is parallel to breadth. If the loop moves away from the current wire in a direction perpendicular to it with a velocity 'v', the magnitude of the e.m.f. in the loop is: (μ0= permeability of free space)
View Solution
