Question

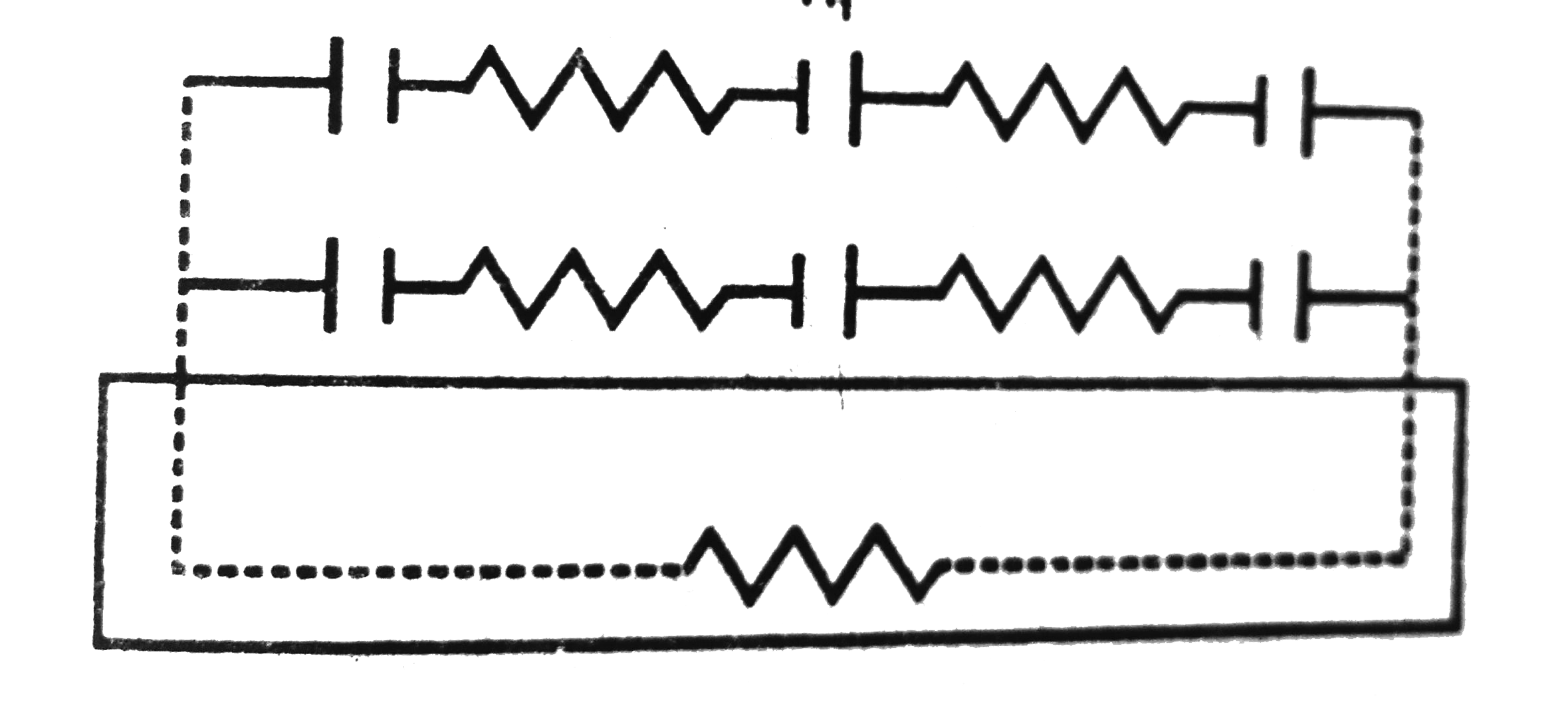
Consider $N=n_1.n_2$ identical cells, each of emf $\left(\epsilon \right)$ and internal resistance r. Suppose $n_1$ cells are joined in series to form a line and $n_2$ such are connected in parallel. The combination drives a current in an external resistance R.

(a) find the current in the external resistance,

(b) Assuming that $n_1$and $n_2$ can be continuously varied, find the relation between $n_1$ , $n_2$ R and r for which the current in R in maximum.

Explanation

Total e.m.f. = ` n_1` E in one row
Total e.m.f. in all rows = `n_1 E`
Total resistance in one row = `n_1`r/`n_2`
Net resistance = `R+ (n_1)r/(n_2)`
` So, Current = R + ((n_1)r/n_2)`
` (b) L = ((n_1)(n_2)E/ n_2 R + n_2 r)`
For, L = max
` (n_1)r + (n_2)R = minimum `
` rArr ((sqrt (n_1)r)- (sqrt(n_2)R))^2 + 2((sqrt(n_1)R(n_2)R)) = min. `
It is minimum when,
` (sqrt(n_1)r) = (sqrt(n_2)R) `
` n_1r = n_2R`
L is maximum when,
` n_1r = n_2R` .