A spherical volume contains a uniformaly distributed charge of density 2.0×104Cm3. Find the electric field at a piont inside the volume at a distance 4.0 cm from the centre.Solution in Gujrati
Given: V = volume charge density
=2.0×(10−4)cm3
Inorder→f∈dthee≤ctricfieldatap∮
4cm=4×(10−2)momthecentre.
Let us assume a concentric spherical
surface inside the sphere.
Now, E×ds=(qε0)
But q=r×43π(r3)
So, E=(qε0.ds)
= (2 xx (10^-4) xx 4 pi (r^3) / (epsilon_0). 3 . 4 pi(r^2))<br>=2×(10−4)×r3ε0
=21.127×(105)NC
=3.0×(105)NC.
Topper's Solved these Questions
Similar Questions
Mark the correct option:
View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
View SolutionA concave mirror having a radius of curvature 40 cm is placed in front of an illuminated point source at a distance of 30 cm from it. Find the location of the image.
View SolutionAn electric dipole consists of charges ±2.0×108C separated by a distance of 2.0×10−3 m. It is placed near a long ilne charge of linear charge density 4.0×10−4Cm−1 as shown in figure (30-W4), Such thet the negative charge is at a distance of 2.0 cm from the line charge. Find the force acting on the dipole.
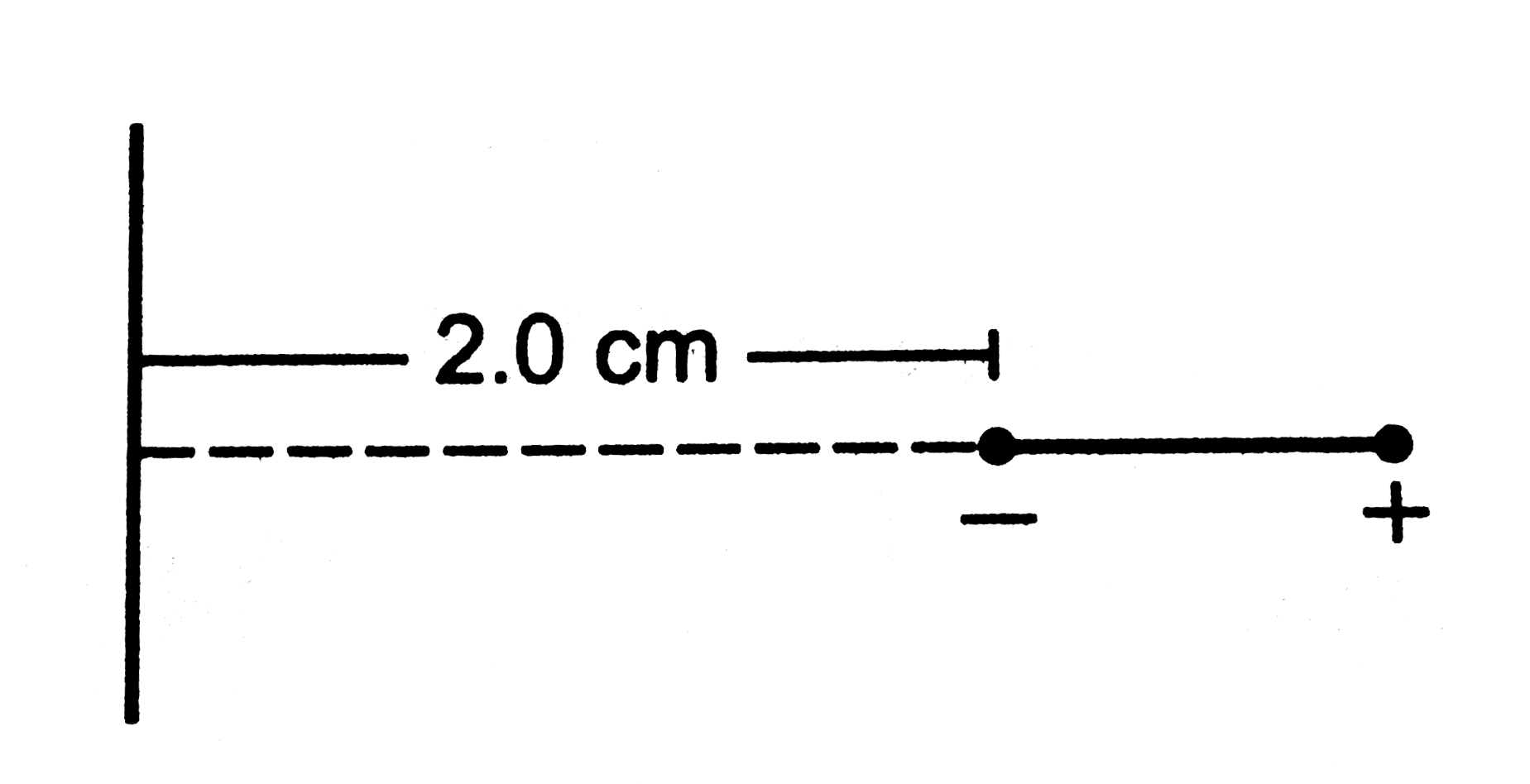
View SolutionA spherical volume contains a uniformaly distributed charge of density 2.0×104Cm3. Find the electric field at a piont inside the volume at a distance 4.0 cm from the centre.
View SolutionFind the magnitude of the electric field at a point 4 cm away from a line charge of density 2×10−6Cm−1.
View SolutionA long cylindrical volume contains a uniformly distributed charge of dendity ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,
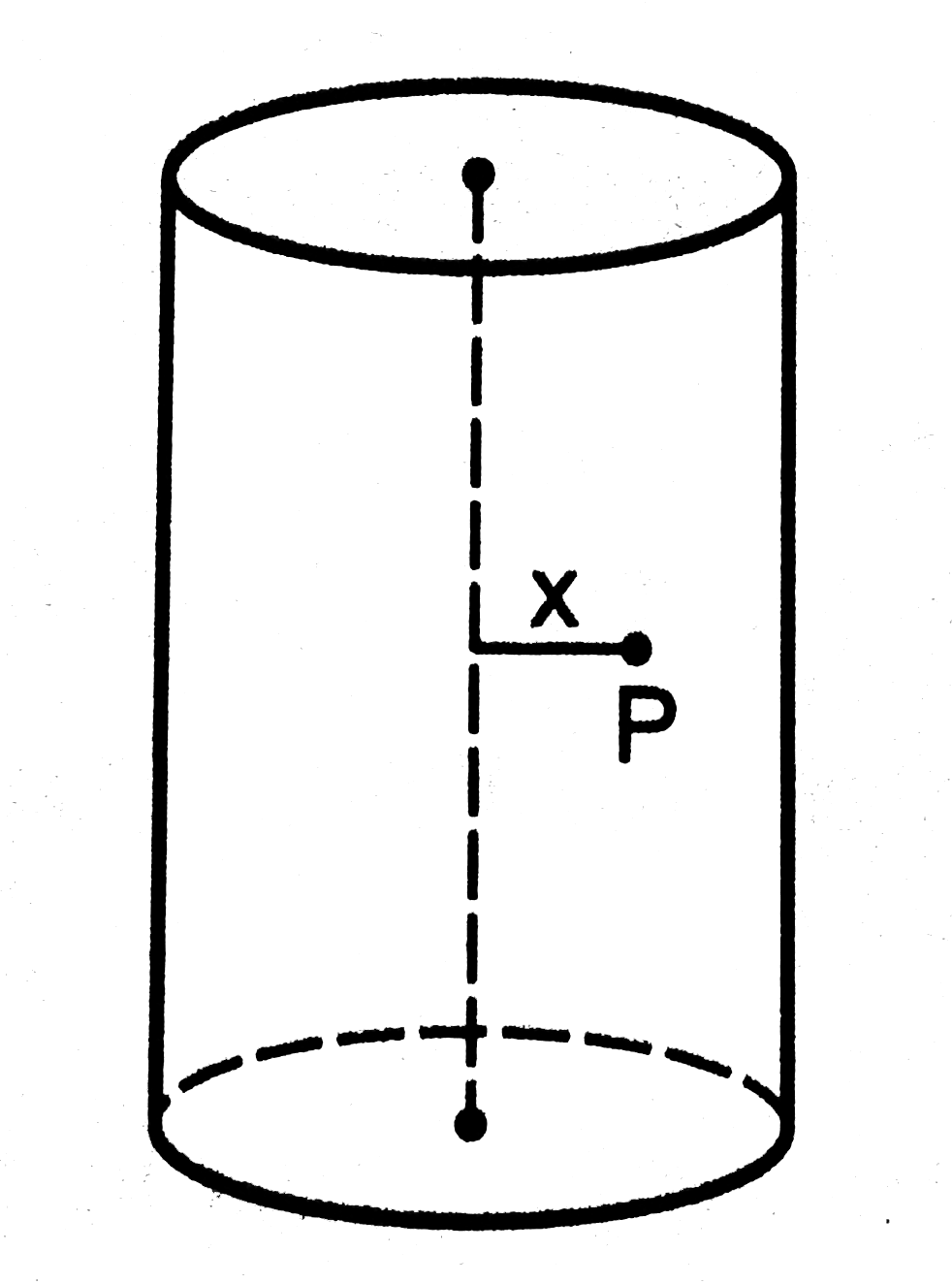
View SolutionA non-conducting spherical ball of radius R contains a spherically symmetric charge with volume charge density rho=kr^(2) where r is the distance form the centre of the ball and n is a constant what should be n such that the electric field inside the ball is directly proportional to square of distance from the centre?
View SolutionCalculate electric field due to a charge uniformly distributed in a spherical volume
View Solutionएक मीटर त्रिज्या के किसी गोले के भीतर विद्युत - आवेश एकसमान रूप से वितरित है तथा प्रत्येक बिंदु पर आवेश का आयतन - घनत्व (volume density of charge ) 2×10−4Cm−3 है । गोले के केंद्र से 4 cm की दुरी पर विद्युतीय क्षेत्र के परिमाण ज्ञात करे ।
View SolutionA spherical valume contains a unifromly distributed charge of density 1.0×10−6C/m3. Find the electrical field (in N/C) at a point inside the volume at a distance 1 mm from the centre. (Let 14π∈0=9×109Nm2C−2)
View SolutionAn electric dipole consists of charges ±2.0×108C separated by a distance of 2.0×10−3 m. It is placed near a long ilne charge of linear charge density 4.0×10−4Cm−1 as shown in figure (30-W4), Such thet the negative charge is at a distance of 2.0 cm from the line charge. Find the force acting on the dipole.
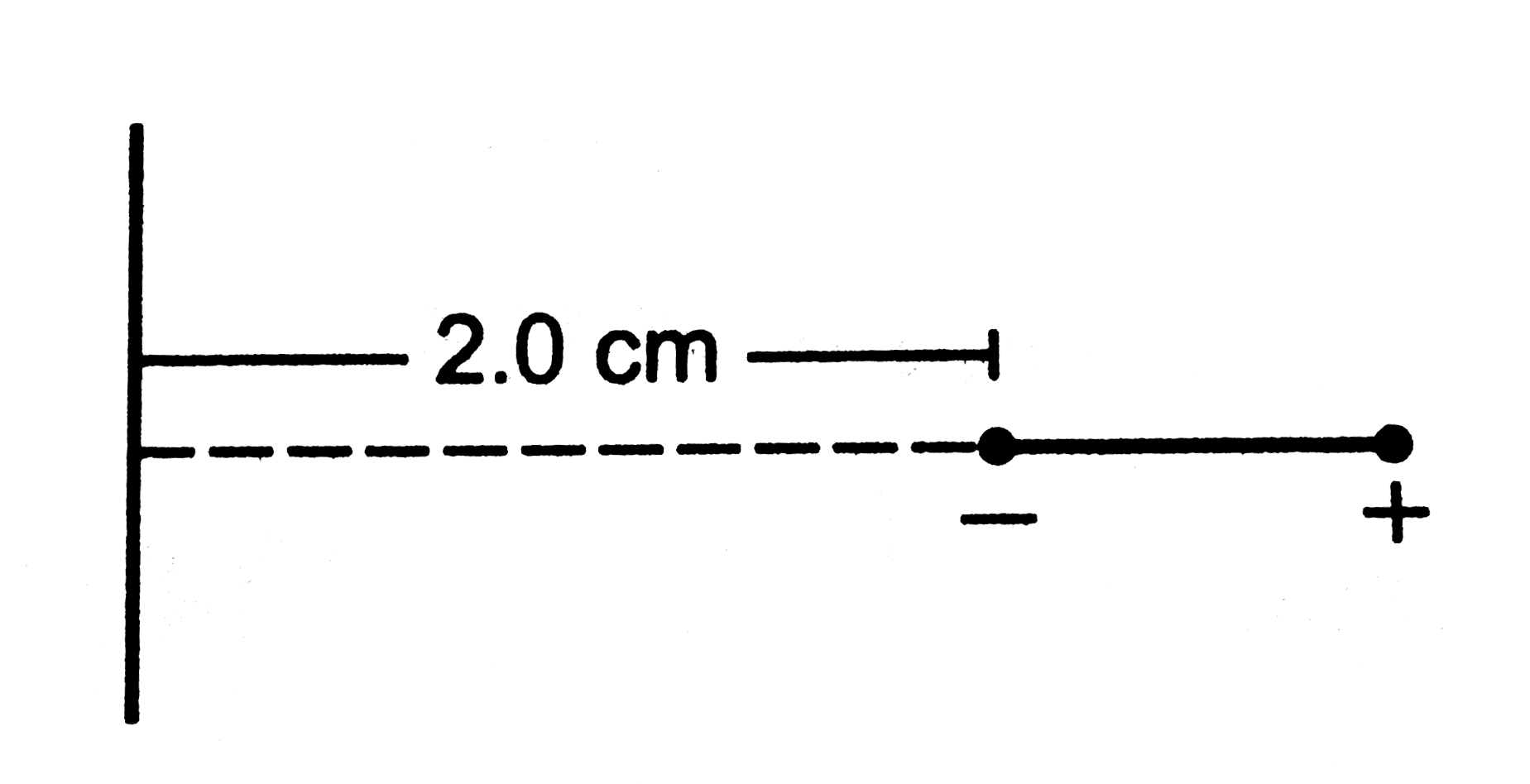
View SolutionA spherical volume contains a uniformaly distributed charge of density 2.0×10−4Cm3. Find the electric field at a piont inside the volume at a distance 4.0 cm from the centre.
View SolutionFind the magnitude of the electric field at a point 4 cm away from a line charge of density 2×10−6Cm−1.
View SolutionA long cylindrical volume contains a uniformly distributed charge of density ρ. Find the electric field at a point P inside the cylindrical volume at a distance x from its axis (figure 30-E5) ,

View SolutionAn electric dipole consists of charges pm 2.0 xx 10^(-8) C separated by a distance of 2.0 xx 10^(-3)m . It is placed near a long line charger of linear charger density 4.0 xx 10^(4) C//m . As shown in figure, such that the negative charge is a distance of 2.0 cm from the line charge. Find the force acting on the dipole
View Solution
