An electric field of 20N/C exists along the x-axis in space. Calculate the potential difference VB−VA where the points A and B are given by
a. A=(0,0),B=(4m,2m)
b. A=(4m,2m),B=(6m,5m)Solution in Gujrati
(a)A=(0,0)B=(4,2)E=20N/C
So,vb−vaE.d=20×(0−4)
(b)A=(4m,2m),B=(6m,5m)
⇒vb−va=e×d
=20×(4−6)2
=20×(−2)=−40vo<.
(c)A=(0,0),b=(6m,5m)
⇒vb−va=e×d
20×(0−6)2
=20×(−6)=120vo<.
Thus potential difference between (0,)and(4,2)is,
dV=−E.dx=−20×4
=−80vo<.
Potentiale≠rgy(ub−ua)betweentheponts=dv×q
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
8 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMACHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Exercises
23 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
Similar Questions
Mark out the correct potons.
View SolutionA discharge tube contains helium at a low pressure. A large potential difference is applied across the tube. Consider a helium atom that has just been ionized due to the detachment of an atomic electron. Find the ratio of the distance travelled by the free electron to that by the positive ion in a short time dt after the ionization.
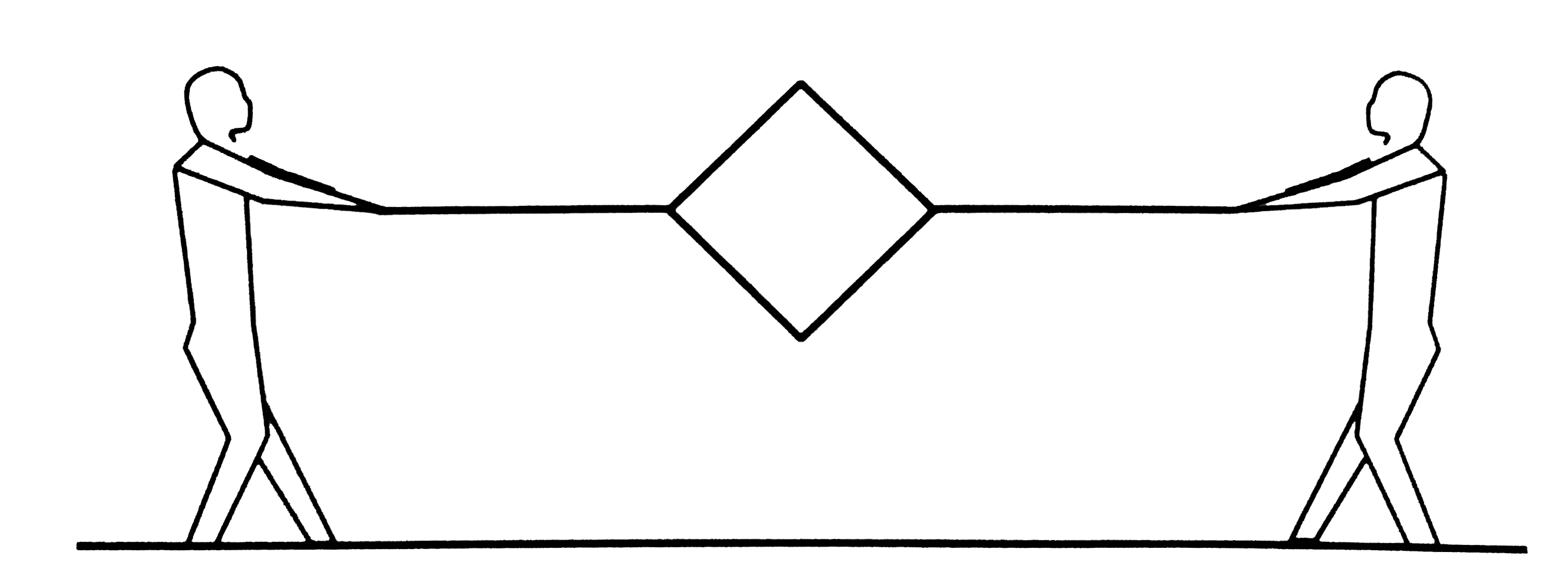
View SolutionShown a metallic square frame of edga a in a vertical plane. A uniform magnetic field B exists in the space in a directon perpendicular to the plane of the figure. Two boys pull the opposite corners of the square ot deform it into a rhombus. They start pulling the corners t t=0 and sisplace the corners at a uniform speed u. (a) find the induced emf in the frame at the instant when the angles at these corners reduce to 60∘. (b) find the induced current in the frame at this instatnt if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
View SolutionAssume that an electric field →E=30x2ˆj exists in space. Then the potential difference VA−VO, where VO is the potential at the origin and VA the potential at x=2m is:
View SolutionAn electric field of 20N/C exists along the x-axis in space. Calculate the potential difference VB−VA where the points A and B are given by
a. A=(0,0),B=(4m,2m)
b. A=(4m,2m),B=(6m,5m)
View SolutionA uniform electric field exists in x−y plane. The potential of points A(−2m,2m),B(−2m,2m) and C(2m,4m) are 4V,16V and 12V respectively. The electric field is
View SolutionA uniform electric field of 30NC−1 exists along the X-axis calculate the potential difference VB−VA between the points A (4m,2m) and B(10m,5m).
View SolutionA uniform electric field is along x-axis. The potential difference V_(A)-V_(B)=10 V is between two points A (2m, 3m) and (4m, 8m). Find the electric field intensity.
View SolutionAn electric field of 10 N/C exists along the x-axis in space. Calculate the potential difference VB−VA where the points A and B are given by -
(a) A = (0, 0), B = (8m, 3m), (b) A = (8m, 3m) , B = (12m, 6m)
(c) A = (0, 0) , B = (12m, 6m)
View SolutionAn electric field of 20 N/C exists along the negative x-axis in space. Calculate the potential difference V_(B)-V_(A) , where the points A and B are given by : (a) A= (0, 0), B=(0, 4m) (b) A=(2m, 1m), B=(4m, 3m)
View SolutionAn electric field →E=Bxˆi exists in space, where B=20V/m2. Taking the potential at (2m, 4m) to be zero, find the potential at the origin.
View SolutionAn electric field of 20N/C exists along the x-axis in space. Calculate the potential difference VB−VA where the points A and B are given by
a. A=(0,0),B=(4m,2m)
b. A=(4m,2m),B=(6m,5m)
View SolutionAssume that an electric field →E=30x2ˆi exists in space. Then the potential difference VA−VO, where VO is the potential at the origin and VA the potential at x=2m is:
View SolutionA field of 100Vm−1 is directed at 30° to positive x-axis. Find (VA−VB) if OA = 2m and OB = 4m

View SolutionAn electric field of 20N/C exists along the x-axis in space. Calculate the potential difference VB−VA where the points A and B are given by
a. A=(0,0),B=(4m,2m)
b. A=(4m,2m),B=(6m,5m)
View SolutionA uniform electric field exists in x−y plane. The potential of points A(−2m,2m),B(−2m,2m) and C(2m,4m) are 4V,16V and 12V respectively. The electric field is
View Solution
