Study the following information carefully and answer the questions given below:
Six cars i.e. M, S, R, T, Q and P which are parked in a parking area in a straight path such that the distance between a car and its adjacent cars is same for all the cars at the instant when they all are parked in a straight line. (i.e. Distance between car Mand car Pis equal to the distance between car Pand car Sif Mand Sare adjacent to P). All cars front side are facing in the north direction. Car Pis parked third to the left of car Q. Car R is parked third to the right of car M. Car P is placed between car S and car R. Car P takes a U turn and started moving and covers distance of 8 unit to reach point A. From point A Car P takes 135∘ right turn and then again covers 10 unit to reach at the point where car Mis parked. Car Pagain covers 4 unit in the north direction from the point Where car M is parked to reach point K. CarQ starts moving in the north direction and covers a certain distance to reach point L.
What is the shortest distance between point K and car Q final position (if the point K and point L lies in a straight line)?
14 unit
15 unit
17 unit
13 unit
The correct Answer is:B
Step 1:- From the given statements, the distance between a car and its adjacent cars is same for all the cars at the instant when they all are parked in a straight line. All cars front side are facing in the north direction. Car R is parked third to the right of car M. Car P is placed between car S and car R so there will be two possible cases

Step II :- Now from the given condition Car Pis parked third to the left of car Q case 1 will be eliminated and we get the final positions of cars in the parking area.
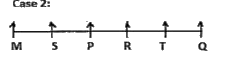
Step III :- Now we will determine the distance between the adjacent cars,
Car P moved 8 unit towards south direction (as it takes U turn from its initial position) to reach point A From point A Car P takes 135o right turn and then again covers 10 unit to reach at the point where car M is parked. Car P again covers 4 unit in the north direction from the last position to reach point K. Car Q starts moving in the north direction and covers a certain distance to reach point L.
Shortest distance between point A and car M initial) is 10 unit.
By using Pythagoras theorem,
The distance between Car M and initial position of car P=√(100−64)=√(36)=6 unit
So 2x = 6 unit
(Where x, is distance between two adjacent cars)
x= 3 unit,
So, we have
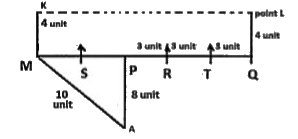
As it is given that Point K and point L lies in a straight line then the distance between both the point is equal to the distance between Car M and Car Q.s initial positions.
Similar Questions
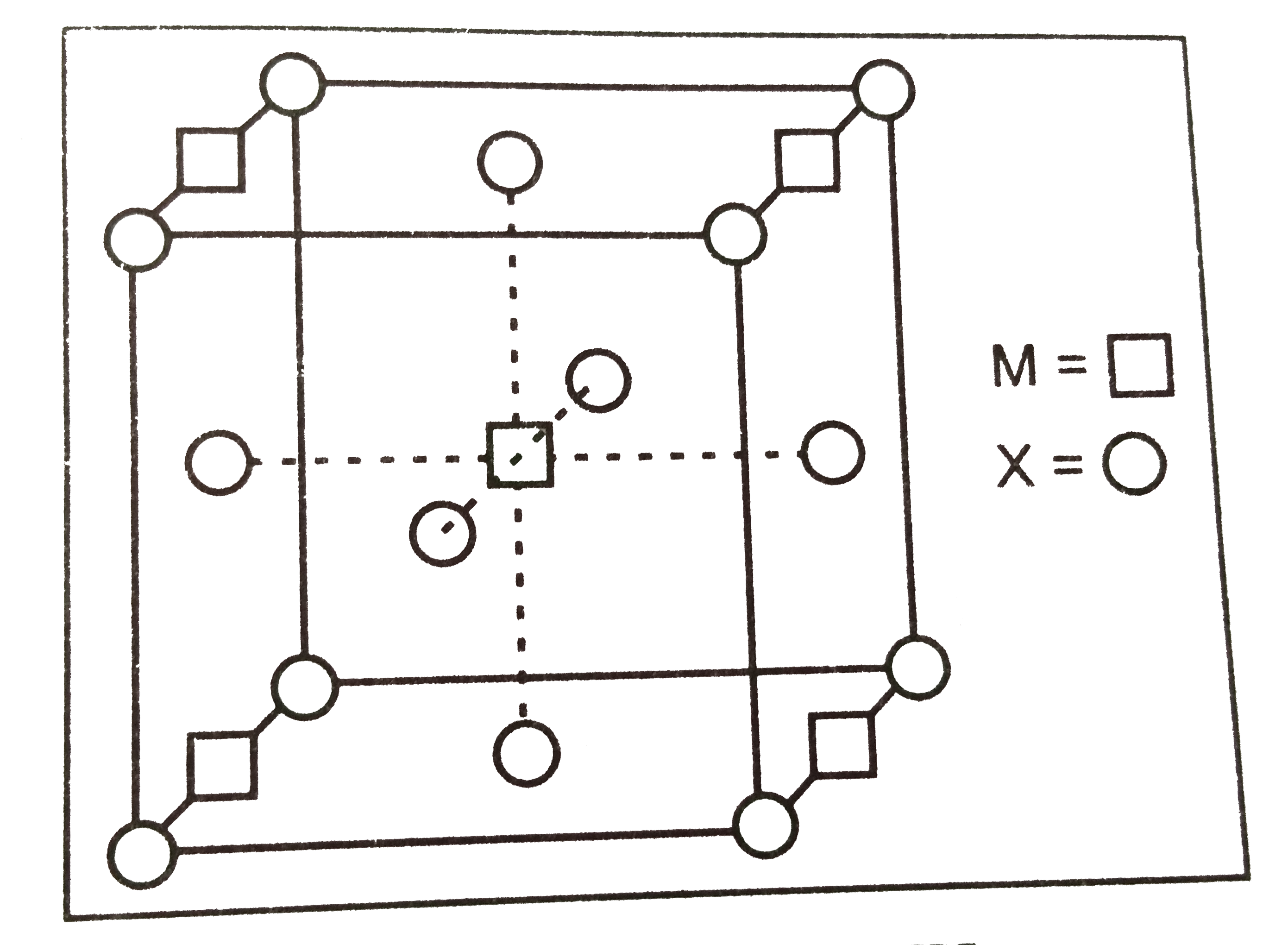
एक यौगिक MpXq में X की घनीय संवृत संकुलन (ccp) व्यवस्था है । इसकी इकाई सेल नीचे दी गई है । यौगिक का मुलानुपाती सूत्र है ।
View Solutionसमान चालकता सेल में लिए गए दो विलयनों A तथा B के प्रतिरोध क्रमशः 50 ओम तथा 100 ओम है । यदि A व B के सामान आयतन मिला दिए जाये तो सामान चालकता सेल में मिश्रण का प्रतिरोध क्या होगा ?
(मोल A व B को मिलाने पर वियोजन की मात्रा में कोई परिवर्तन नहीं होता है)
View Solutionयदि A और B दो घटनाएँ इस तरह से हों कि P(A)=13,P(B)=14,P(A∩B)=15 तो P(A/B)=
View Solutionनिम्नलिखित कथनों पर विचार करें :
कथन I : यदि A और B प्रतिदर्श समष्टि S के संगत दो घटनाएँ ऐसा है कि P(A)=0.2 और P((B)=0⋅8 तो A⋃B एक सुनिश्चित घटना है |
कथन I : यदि A और B परस्पर अपवर्ती हों तो P(A)+P(B)=1 इन कथनो में :
View Solutionयदि l, m, n एक सरल रेखा की दिककोज्याएँ है, तो
View Solutionएक सरल रेखा (2,-1,3) से गुजरती है और इसके दिक्अनुपात 3,-1,2 है | इस रेखा के समीकरण है
View Solutionरामू एक सब्जी उत्पादर हैं । वह अपने उपजाऊ भूमि में टमाटर लगाकर उच्च पैदावर प्राप्त करता हैं । लेकिन उसके खेत से मण्डी की दूरी अधिक थी तथा परिवहन के साधन भी उपलब्ध नहीं थे , जिसके परिमाणस्वरुप विलंब के कारण टमाटर सड़ जाते थे तथा बाजार में मूल्य नही मिलते थे ।
जब उसने कृषि विश्वविद्यालय में पढ़ने वाले अपने मित्र को समस्या से अवगत कराया तब मित्र ने उसे पारजीनी टमाटर की किस्म उगाने को कहा जो कि विलम्ब से पकता हैं ।
उपर्युक्त गद्यांश को ध्यानपूर्वक पढ़ने के बाद निम्न - लिखित प्रश्नों के उत्तर दीजिये - (i) पारजीनी (Transgenic) क्या हैं ?
(ii) पारजीनी टमाटर का उत्पादन कैसे किया जाता हैं ?
(iii) रामू के मित्र व्दारा किन मूल्यों का प्रदर्शन किया गया ?
View SolutionP and Q are the middle points of two chords (not diameters) AB and AC respectively of a circle with centre at a point O. The lines OP and OQ are produced to meet the circle respectively at the points R and S. T is any point on the major arc between the points R and S of the circle. If ∠BAC=32∘,∠RTS = ?
View Solution
