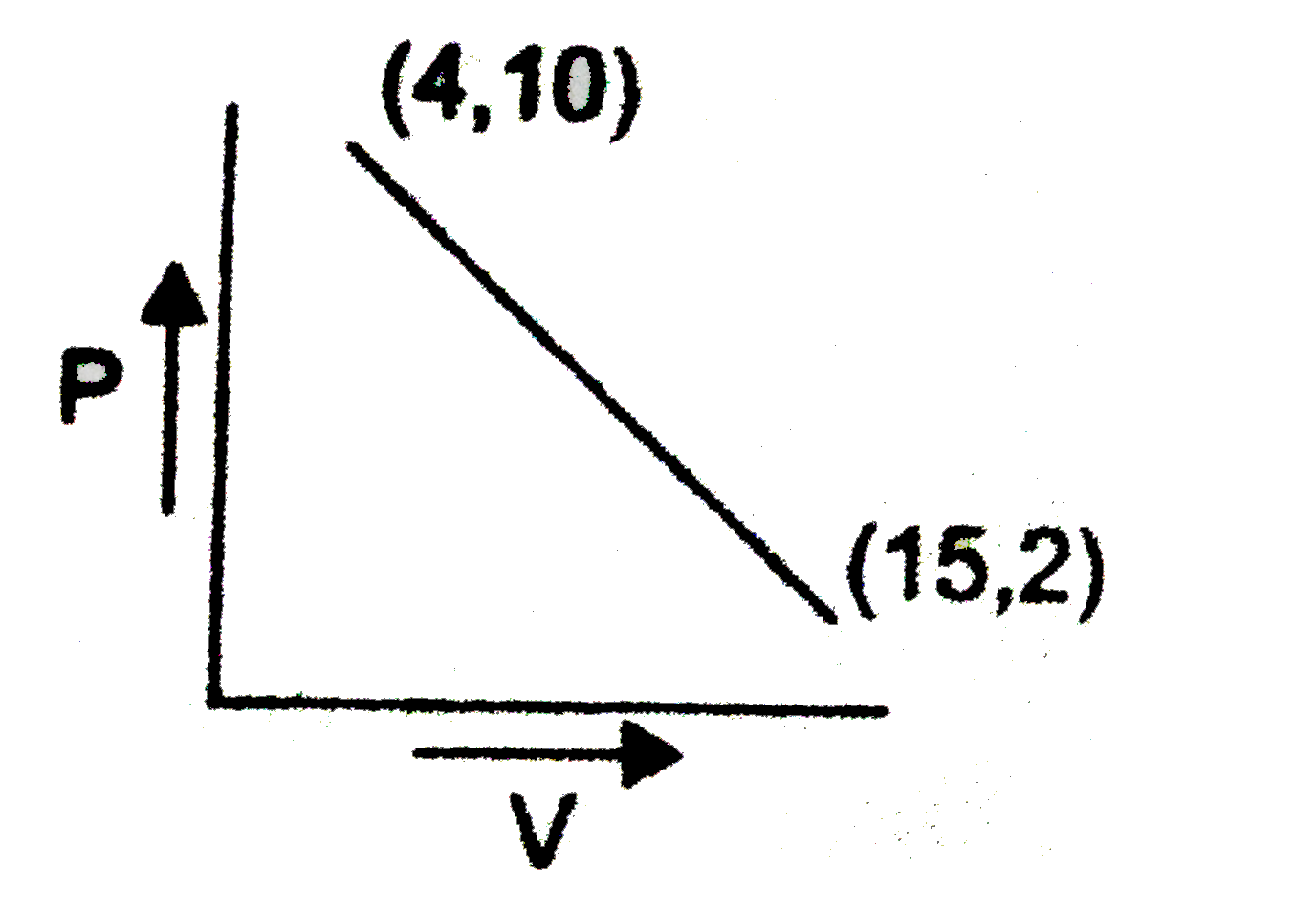
One mole of a gas changed from its initial state (15L,2 atm) to final state (4L,10 atm) reversibly. If this change can be represented by a straight line in P - V curve maximum temperature (approximate), the gas attained is x×102K. Then find the value of x. Solution in Telugu
The correct Answer is:7
Equation of line
P−2=10−24−15(V−15)
P−2=811(V−15)
P=2−8V11+15×811
P=(14211−8V11)
f(T)=1nR(142V11−8V211)
d(F(T))dV=1nR(14211−8V211)=0
V=14211×16=8.875
P=14211−811×8.87516=7111
TMax=PVnR=7111×14216×0.0821=700
=7×102K
Topper's Solved these Questions
- GASEOUS STATEBOOK - NARENDRA AWASTHICHAPTER - GASEOUS STATEEXERCISE - Level 3 - Passage
1 Videos
- ELECTROCHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - ELECTROCHEMISTRYEXERCISE - Level 3 - Subjective Problems
1 Videos
- IONIC EEQUILIBRIUMBOOK - NARENDRA AWASTHICHAPTER - IONIC EEQUILIBRIUMEXERCISE - Assertin-Reason Type Questions
1 Videos
Similar Questions
Collision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
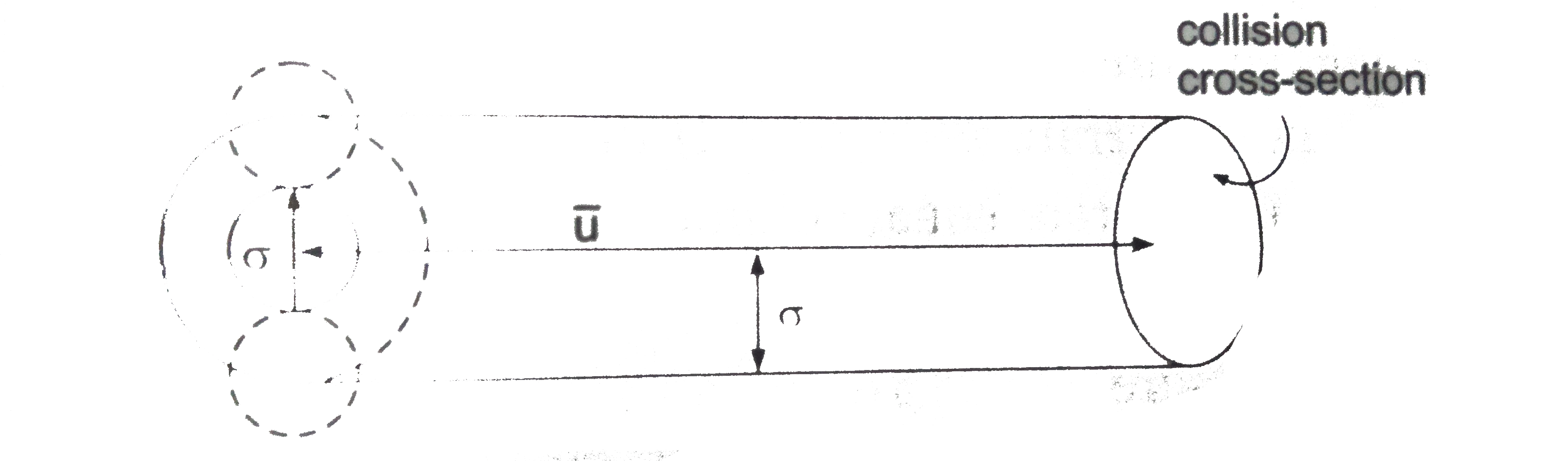
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.
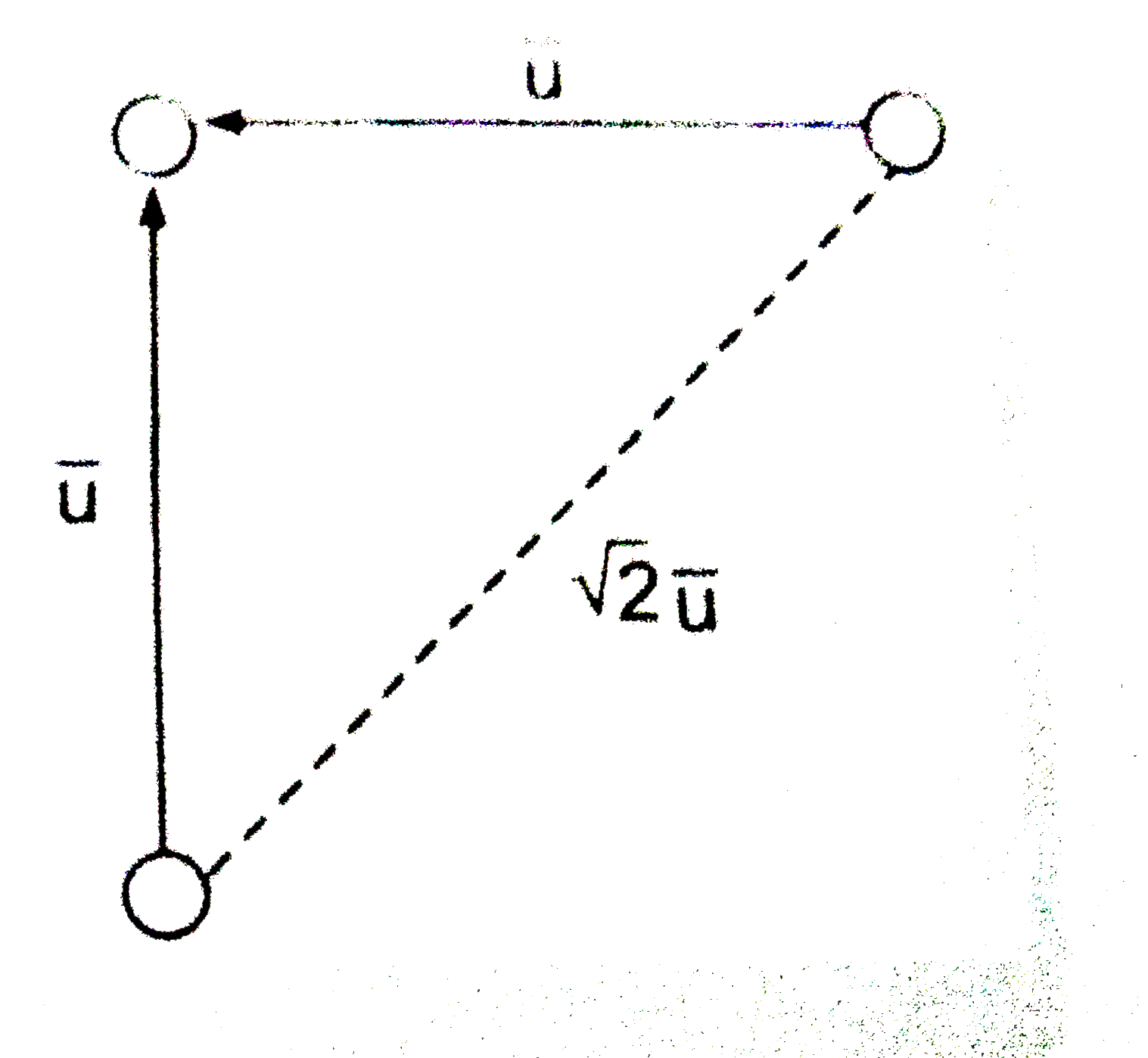
Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
For a given gas the mean free path at a particular pressure is :
View SolutionA solution containing 1MXSO4(aq) and 1MYSO4(aq) is electrolysed. If conc. Of X2+ is 10−zM when deposition Y2+ and X2+ starts simultaneously, calculate the value of Z.
Given: 2.303RTF=0.06
E∘x2+|X=−0.12V,E∘Y2+|Y=−0.24V
View SolutionSTATEMENT-1: All strong monoprotic acid with same concentration in dilute solution show same pH.
STATEMENT-2: Water shows levelling effect.
View Solution1 mol of a gas is changed from its initial state (15 L, 2 atm) to final state (4 L, 10 atm) . If this change can be represented by a straight line in P-V curve, calculate the maximum temperature that, the gas attained.
View SolutionTwo moles of an ideal gas undergo the following process :
(a) a reversible isobaric expansion from (P atm, VL) to (P atm , 2VL).
(b) a reversible isochoric change of state from (P atm , 2V,L) to (P/2 atm, 2VL)
(c) a reversible isothermal compression from (P/2 atm, 2VL) to (P atm, VL).
Sketch with labels each of the processes on the same P−V diagram.
View SolutionOne mole of an ideal gas (C_(v,m)=(5)/(2)R) at 300 K and 5 atm is expanded adiabatically to a final pressure of 2 atm against a constant pressure of 2 atm. Final temperature of the gas :
View SolutionOne mole of an ideal gas undergoes a process (10L, 4atm) to (4L, 10 atm ). The process may be represented by straight line in P-V diagram The only incorrect statement is : (R = 0.08 L-atm/K-mol)
View SolutionOne mole of an ideal gas (C_(v,m)=(5)/(2)R) at 300 K and 5 atm is expanded adiabatically to a final pressure of 2 atm against a constant pressure of 2 atm. Final temperature of the gas is :
View SolutionOne mole of a gas changed from its initial state (15L,2 atm) to final state (4L,10 atm) reversibly. If this change can be represented by a straight line in P - V curve maximum temperature (approximate), the gas attained is x×102K. Then find the value of x.
View SolutionWhen a sample of ideal gas is changed from an initial state to a final state, various curves can be plotted for the process like P-V curve, V-T curve,P-T curve etc. For example, P-V curve for a fixed amount of an ideal gas at constant temperature is a rectangular hyperbola, V-T curve for a fixed amount of an ideal gas at constant volume is again a straight line. However, the shapes may vary if the constant parameters are also changed. Now, answer the following questions : Two moles of an ideal gas is changed from its initial state (16 atm, 6L) to final state (4 atm, 15L) in such a way that this change can be represented by a straight line in P-V curve.The maximum temperature attained by the gas during the above change is :(Take : R=1/12L atm K^(-1) "mol"^(-1) )
View SolutionA system containing real gas changes it's state from state -1 to state - 2 . State -1 ( 2atm, 3L,300K) State-2 (5 atm, 4L,500K) If change in internal energy = 30 L atm then calculate change in enthalpy.
View SolutionAt 302 K, one mole of an ideal gas is compressed isothermally and reversibly from a pressure of 2 atm to 10 atm. The values of ΔU and q respectively will be _______ .
View SolutionOne mole of non− ideal gas undergoes a change of state (1.0atm,3.0L,200K) to (4.0atm,5.0L,250K) with a change in internal energy (ΔU)=40L−atm. The change in enthalpy of the process in L−atm,
View SolutionOne mole of an ideal gas (C_(v,m)=(5)/(2)R) at 300 K and 5 atm is expanded adiabatically to a final pressure of 2 atm against a constant pressure of 2 atm. Final temperature of the gas is :
View SolutionOne mole of a gas changed from its initial state (15L,2 atm) to final state (4L,10 atm) reversibly. If this change can be represented by a straight line in P - V curve maximum temperature (approximate), the gas attained is x xx10^(2) K. Then find the value of x.
View SolutionAt 300 K, one mole of an ideal gas is compressed isothermally and reversibly from a pressure of 2 atm to 10 atm. The values of ΔU and q respectively will be _______ .
View Solution
