Figure shows a rod of length l resting on a wall and the floor. Its lower end A is pulled towards left with a constant velocity v. Find the velocity of the other end B downward when the rod makes an angle θ with the horizontal.

In such type of problems, when velocity of one part of a body is given and that of other is required, we first find the relation between the two displacement, then differentiate them with respect to time. Here if the distance from the corner to the point A is x and up to B is y. Then v=dxdt&vB=−dydt
(-sign denotes that y is decreasing)
Further, x2+y2=l2
Differentiating with repsect to time t
2xdxdt+2ydydt=0 xv=yvB
vB+(v)xy=vcotθ
Similar Questions
The block A is moving downward with constant velocity v0. Find the velocity of the block B. When the string makes an angle θ with the horizontal

View SolutionA uniform rod of length l is spinning with an angular velocity ω=2vl while its centre of mass moves with a velocity v. Find the velocity of the end of the rod.

View SolutionA rod of length l is moving in a vertical plane (x−y) when the lowest point A of the rod is moved with a velocity v. find the a angular velocity of the rod and b velocity of the end B.

View SolutionA rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

View SolutionA light rigid rod of length l is constrained to move in a vertical plane, so that its ends are along the x and y axes respectively. Find the instantaneous axis of rotation of the rod when it makes an angle θ with horizontal.

View SolutionA rod of length 'l' is inclined at an angle 'θ' with the floor against a smooth vertical wall. If the end A moves instantaneously with velocity v1, what is the velocity of end B at the instant when rod makes 'θ' angle with the horizontal.
View SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionA rod of mass m and length l is kept on a surface that has no friction. If a ball comes & hits the lower end with a velocity v, then the velocity of centre of mass will be

View Solution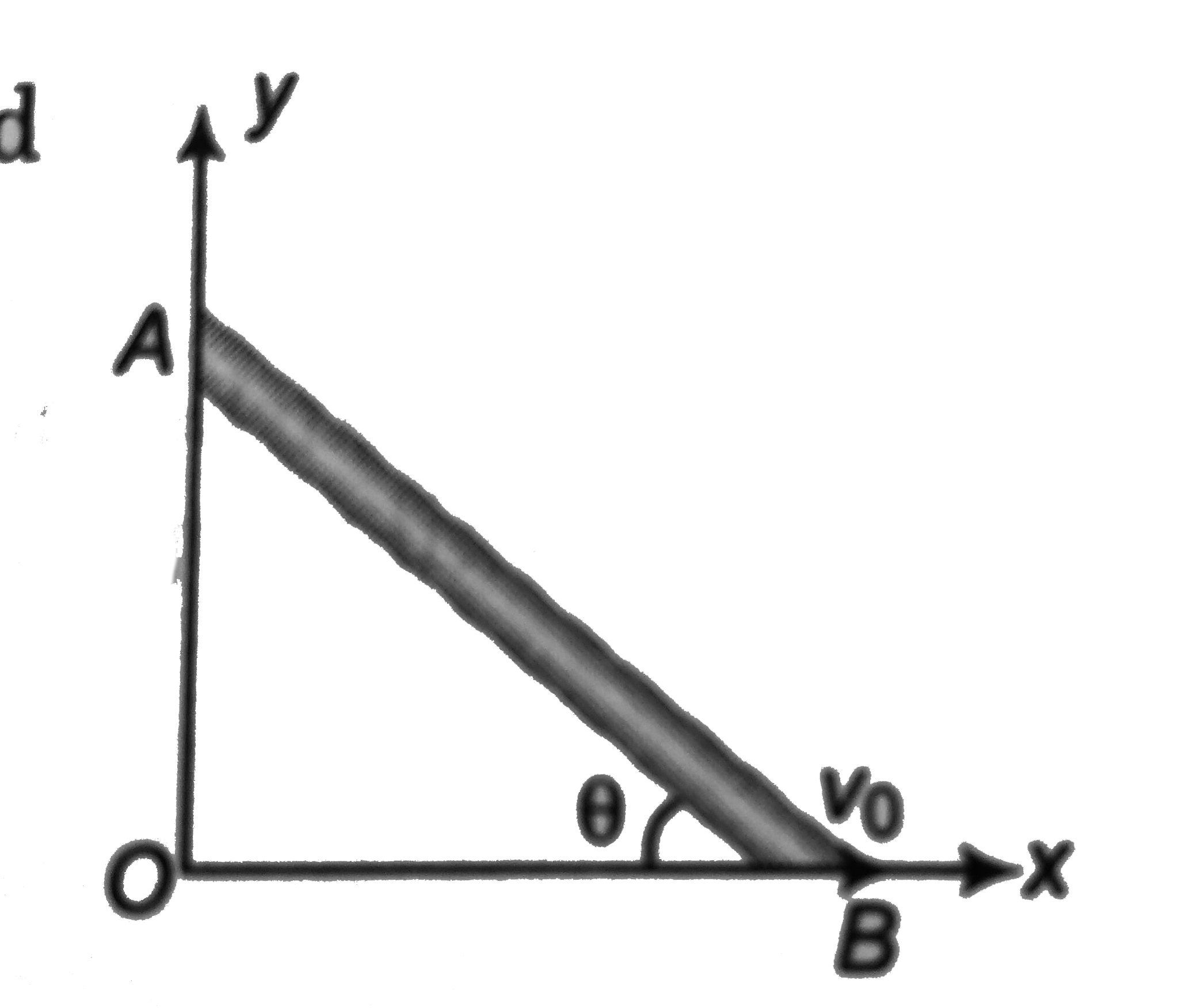
The end B of the rod AB which makes angle θ with the floor is being pulled with a constant velocity vv as shown. The length of the rod is l.
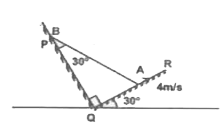
View SolutionA rod of length L is sliding on a frictionless surface as shown in the figure. Velocity of end A is 4m/s along the wall. Find the velocity of end B, when end B makes 30∘ with wall PQ.
View Solution
