A man of height 1.47 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as where is the refractive index of air near the road a /m. What is the apparent length of the road man is able to sec?
700m
2000m
infinite distance
The correct Answer is:B
Step by step video & image solution for A man of height 1.47 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as mu=mu_(0)sqrt((1+ay)) where mu_(0) is the refractive index of air near the road a =1.5xx10^(-6)/m. What is the apparent length of the road man is able to sec? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE-II (LEVEL-II (ADVANCED) LINKED COMPREHENSION TYPE QUESTIONS))
8 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE-II (LEVEL-II (ADVANCED) MATRIX MATCHING TYPE QUESTIONS))
1 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE-II (LEVEL-I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS))
17 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
A man of height 1.47 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as μ=μ0√(1+ay) where μ0 is the refractive index of air near the road a =1.5×10−6/m. What is the apparent length of the road man is able to sec?
View SolutionA man of height 2 m stands on a straight road on a hot day. The vertical temperature in the air results in a variation of refractive index with height y as μ=μ0√(1+ay) where μ0 is the refractive index of air near the road and a=2×10−6/m. What is the actual length of the road, man is able to see
View SolutionWhat is the refractive index in a medium where the speed of light is 1.5×108 m/s ?
View SolutionA man of height 2.0m is standing on a level road because of temprature variation the refractive index of air is varying as μ=√1+ay, where y is height from road. If a=2.0×10−6m−1. Then, find distant point that he can see on the road.
View SolutionDue to a vertical temperature gradient in the atmosphere, the index of refraction varies. Suppose index of refraction varies as n=n0√1+ay, where n0 is the index of refraction at the surface and a=2.0×10−6m−1 . A person of height h=2.0m stands on a level surface. Beyond what distance will he not see the runway?

View SolutionA long rectangular slab of transparent medium of thickness d placed on a table with its length parallel to the x-axis and width parallel to the axis. A ray of light travelling inair makes a near normal incidence on the slab as shown. Taking the point of incidence as orign (0,0,0). The refraction index μ of the medium varies as μ=μ01−(xr) where μ1 and r(>d) are constants. The refractive index of air is μ0
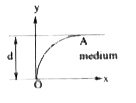
The x-coordinate of the point A where the ray intersects the upper surface of the slab air boundary is
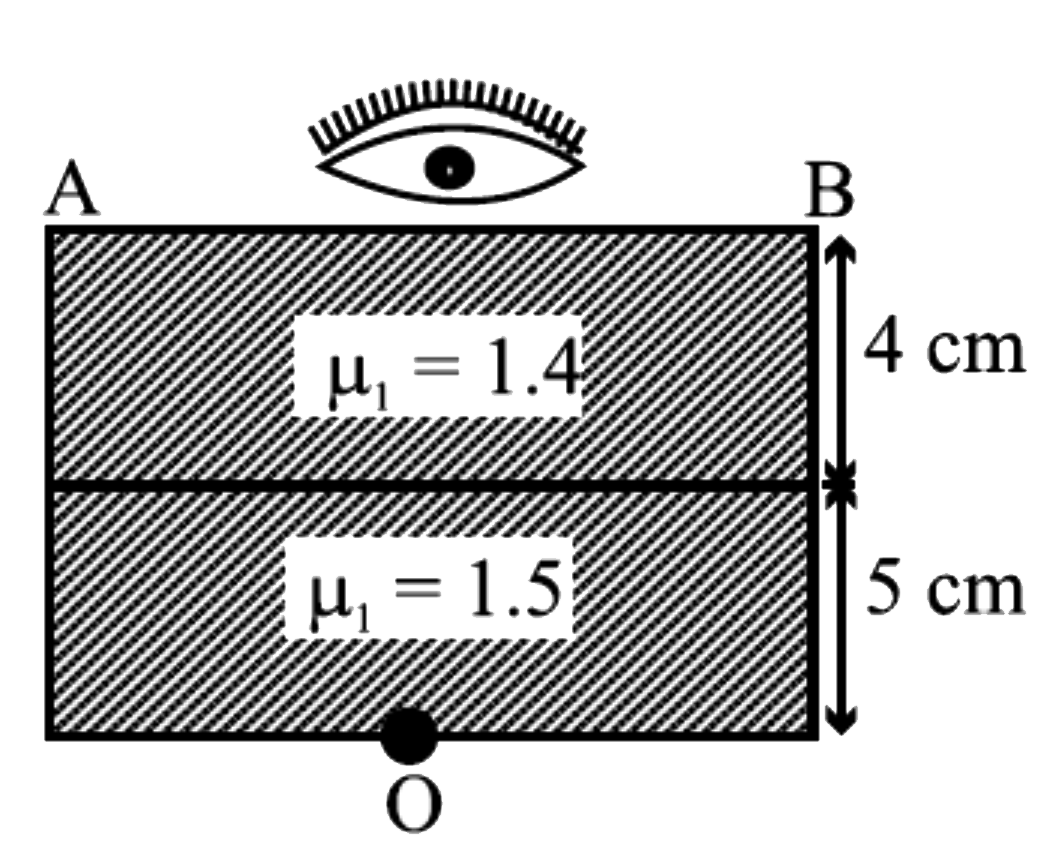
View SolutionThe apparent depth of an object O from AB is
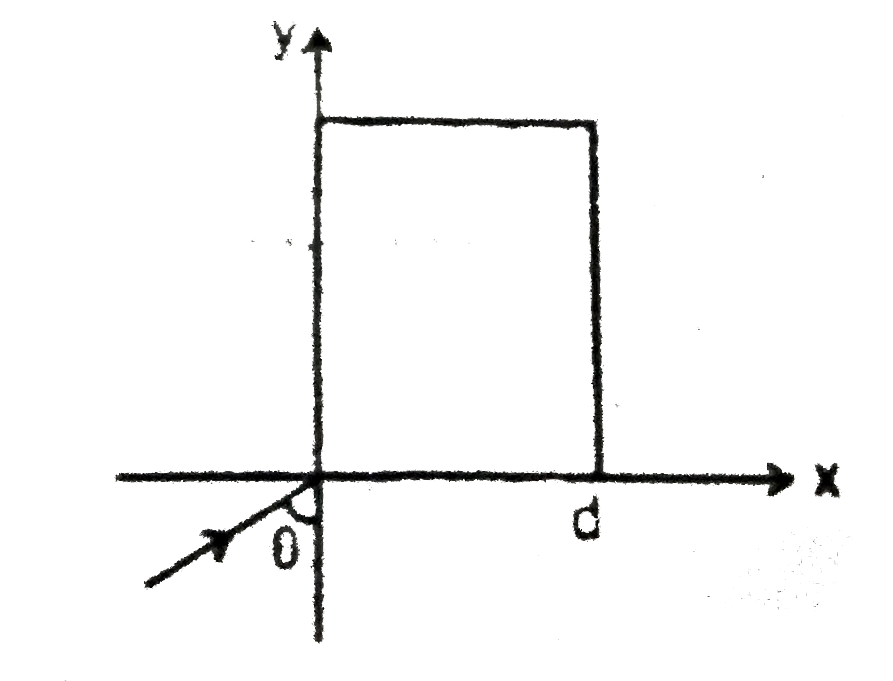
View SolutionA ray hits the y-axis making an angle θ with y-axis as shown in the figure. The variation of refractive index with x-coordinate is μ=μ0(1−xd) for 0≤x≤d(1−1μ0) and μ=μ0 for x<0, where d is a positive constant. The maximum x-coordinate of the path traced by the ray is
View SolutionThe figure shows a transparent slab of length m placed in air whose refractive index in x direction varies as μ=1+x2(0<x<1). The optical path length of ray R will be

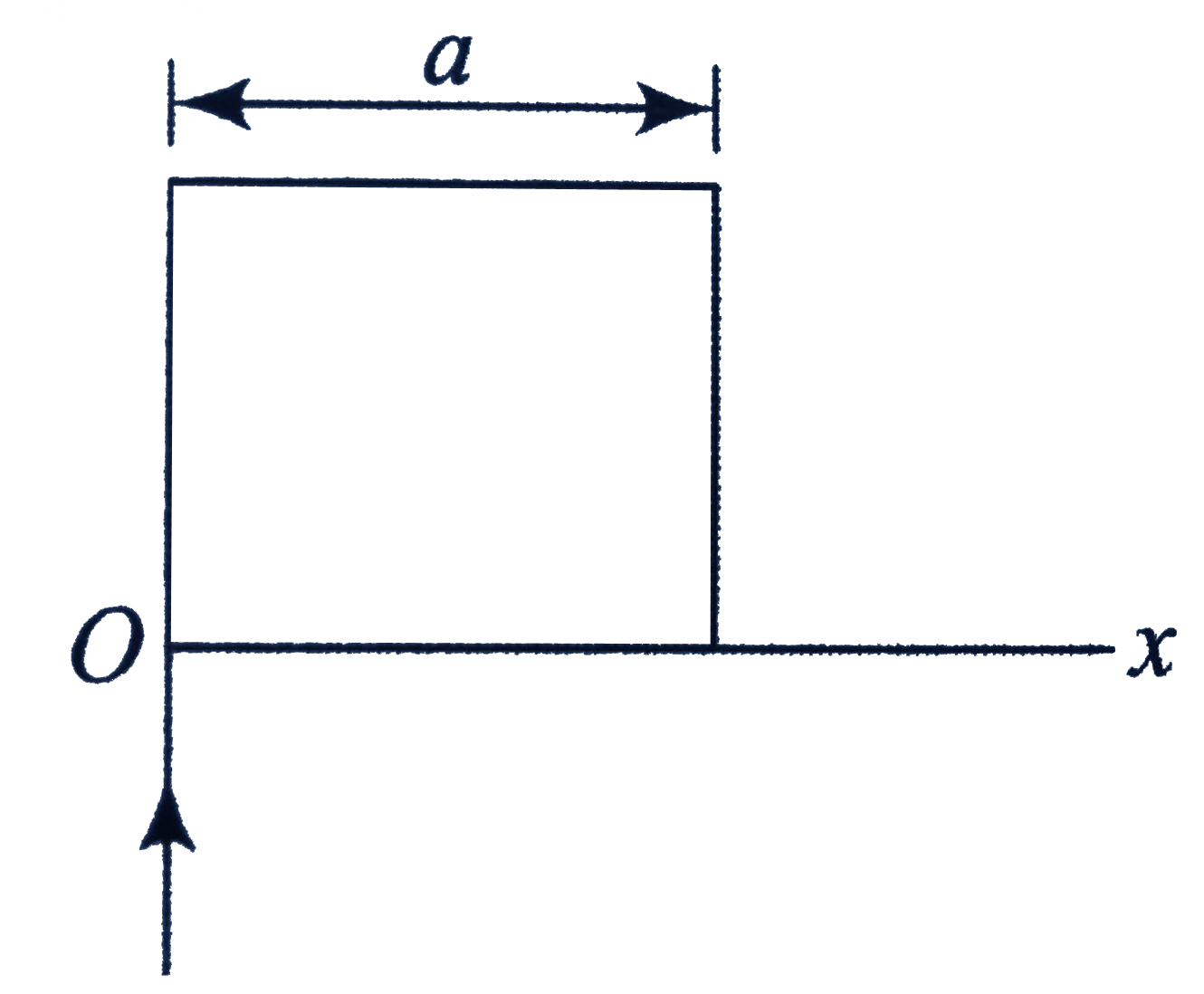
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
View Solution
