Vector →A is 2cm long and is 60∘ above the x-axis in the first quadrant. Vector →B is 2cm long and is 60∘ below the x-axis in the fourth quadrant. The sum →A+→B is a vector of magnitudes
→R=→A+→B
R=2cos600ˆi+2sin60ˆj+2cos60ˆi−2sin60ˆj
→R=4cos600ˆi=2ˆi
∴2cm, along x-axis
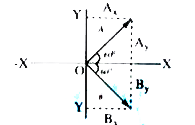
Similar Questions
Vector →A is 2cm long and is 60∘ above the x-axis in the first quadrant. Vactor →B is 2cm long and is 60∘ below the x-axis in the fourth quadrant. The sum →A+→B is a vector of magnitudes
View SolutionVector →A is 2 cm long and is 60° above the x - axis in the first quadrant, vector →B is 2cm long and is 60° below the x - axis in the fourth quadrant. Find →A+→B
View Solution→Aand→B are two vectors such that →A is 2 m long and is 60∘ above the x - axis in the first quadrant →B is 2 m long and is 60∘ below the x - axis in the fourth quadrant .
Draw diagram to show →a+→B,→A−→Band→B−→A
(b) What is the magnitude and direction of →A+→B,→A−→Band→B−→A
View SolutionIf →aand→b are the unit vectors and θ is the angle between them, then →a+→b is a unit vector if
View SolutionIf a vector →A is parallel to another vector →B then the resultant of the vector →A×→B will be equal to
View SolutionA vector →B which has a magnitude 8.0 is added to a vector →A which lies along the x-axis. The sum of these two vector is a third vector which lies along the y-axis and has a magnitude that is twice the magnitude of →A. Find the magnitude of →A
View SolutionA vector →A of length 10 units makes an angle of 60∘ with a vector →B of length 6 units. Find the magnitude of the vector difference →A−→B & the angles with vector →A.
View SolutionLet −−→AB be a vector in two dimensional plane with magnitude 4 units. And making an anle of 600 with x-axis, and lying in first quadrant. Find the components of −−→AB in terms of unit vectors ˆiandˆj. so verify that calculation of components is correct.
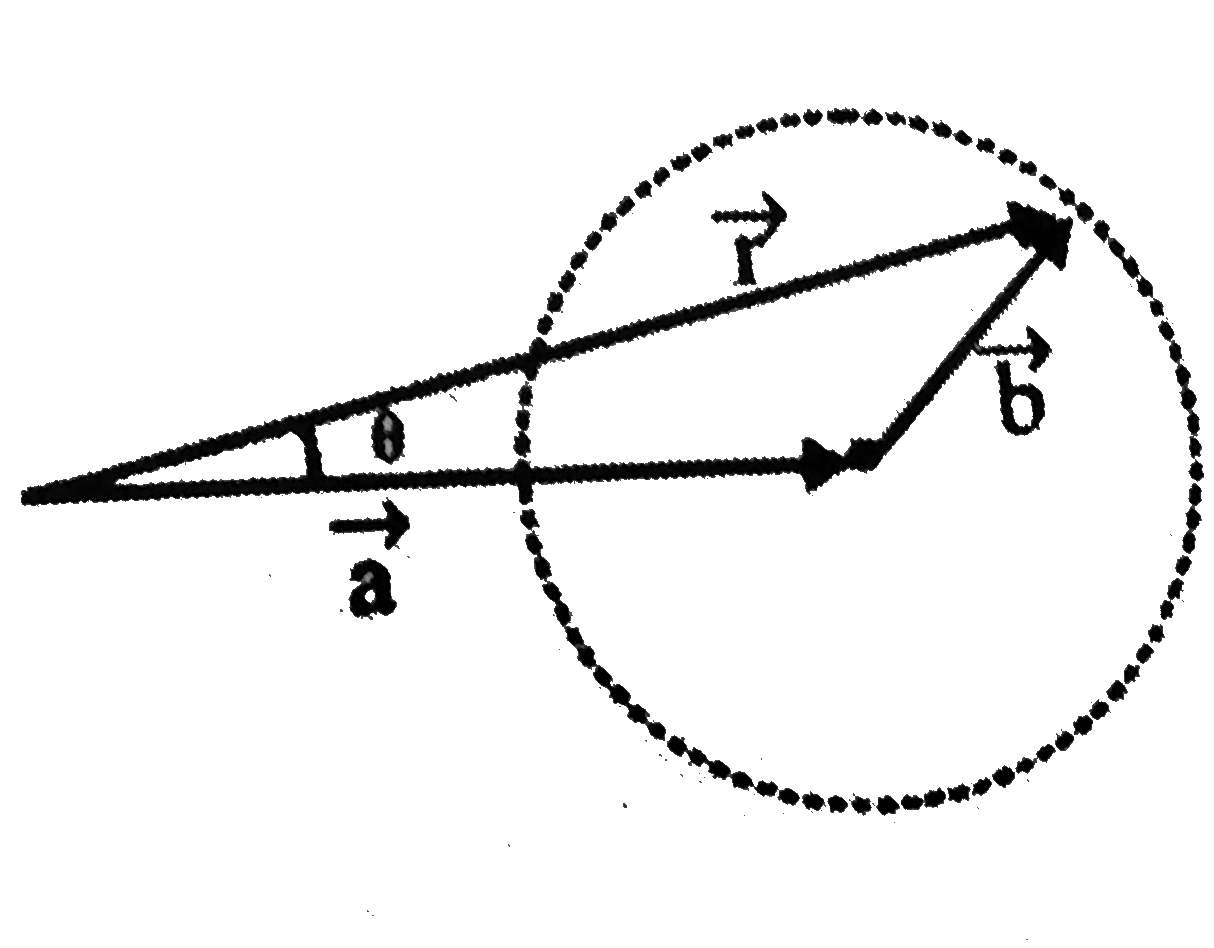
View SolutionKeeping one vector constant, if direction of other to be added in the first vector is changed continuously, tip of the resultant vector describes a circles, In the following figure vector →a is kept constant. When vector →b addede to →a changes its direction, the tip of the resultant vector →r=→a+→b describes circles of radius b with its centre at the tip of vector →a. Maximum angle between vector →a and the resultant →r=→a+→b is
View SolutionIf the vectors →a+→b,→b+→c and →c+→a are coplanar, then prove that the vectors →a,→b and →c are also coplanar.
View Solution
