A block of mass m is arranged on the wedge as shown in figure . The wedge angle is θ. If the masses of pulley and thread and negligible and friction is absent , find the acceleration of the wedge
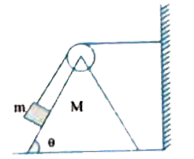
It is obvious that when block m moves downward along the incline of wedge, the wedge moves to the right . As the length of thread is constant, the distance traversed by wedge along the incline is equal to distance traversed by wedge to the right . This implies that acceleration of wedge to the right is equal to downward acceleration of wedge .
Let a be the acceleration of wedge to the right .
Then the force acting on the block m are
(i) weight mg acting vertically downward
(ii) normal reaction R1
(iii)tension T (up the incline )
(iv)Fictitious force ma to the left .
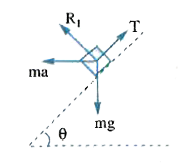
The free body diagram of mass m is shoen in figure .
For motion of block .m. on inclined plane
mgsinθ+macosθ−T=ma ....(1)
As mass .m. does not breaks off the inclined plane , therefore for forces on .m. normal to inclined plane
R1+masinθ=mgcosθ ....(2)
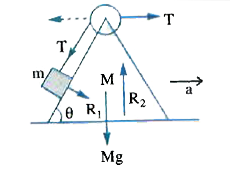
The forces acting on the wedge are
(i) weight Mg downward
(ii) normal reactionof ground on wedge =R2
(iii) normal reaction of block on wedge =R1
(iv) tension (T,T) in string .
The free body diagram of wedge is shown in figure .
For motion of wedge in horizontal direction
R1sinθ+T−Tcosθ=mg ....(4)
From (1),
T=mgsinθ+macosθ−ma ....(5)
From (2), R1=mgcosθ−masinθ ....(6)
substituting these values in (3) , we get
(mgcosθ−masinθ)sinθ+(mgsinθ+macosθ−ma)(1−cosθ)=Ma
or {M+msin2θ+m(1−cosθ)2}a
=mgcosθsinθ+mgsinθ(1−cosθ)
a=mgsinθM+msin2θ+m(1−2cosθ+cos2θ)=mgsinθM+m(sin2θ+1−2cosθ+cos2θ)
∴a=mgsinθM+2m(1−cosθ)
Similar Questions
A block of mass m is at rest on a rough wedge as shown in figure. What is the force exerted by the wedge on the block?

View SolutionA block of mass m is at rest on a rought wedge as shown in figure. What is the force exerted by the wedge on the block?

View SolutionA block of mass m is at rest on a rough wedge as shown in figure. What is the force exerted by the wedge on the block?

View SolutionA pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
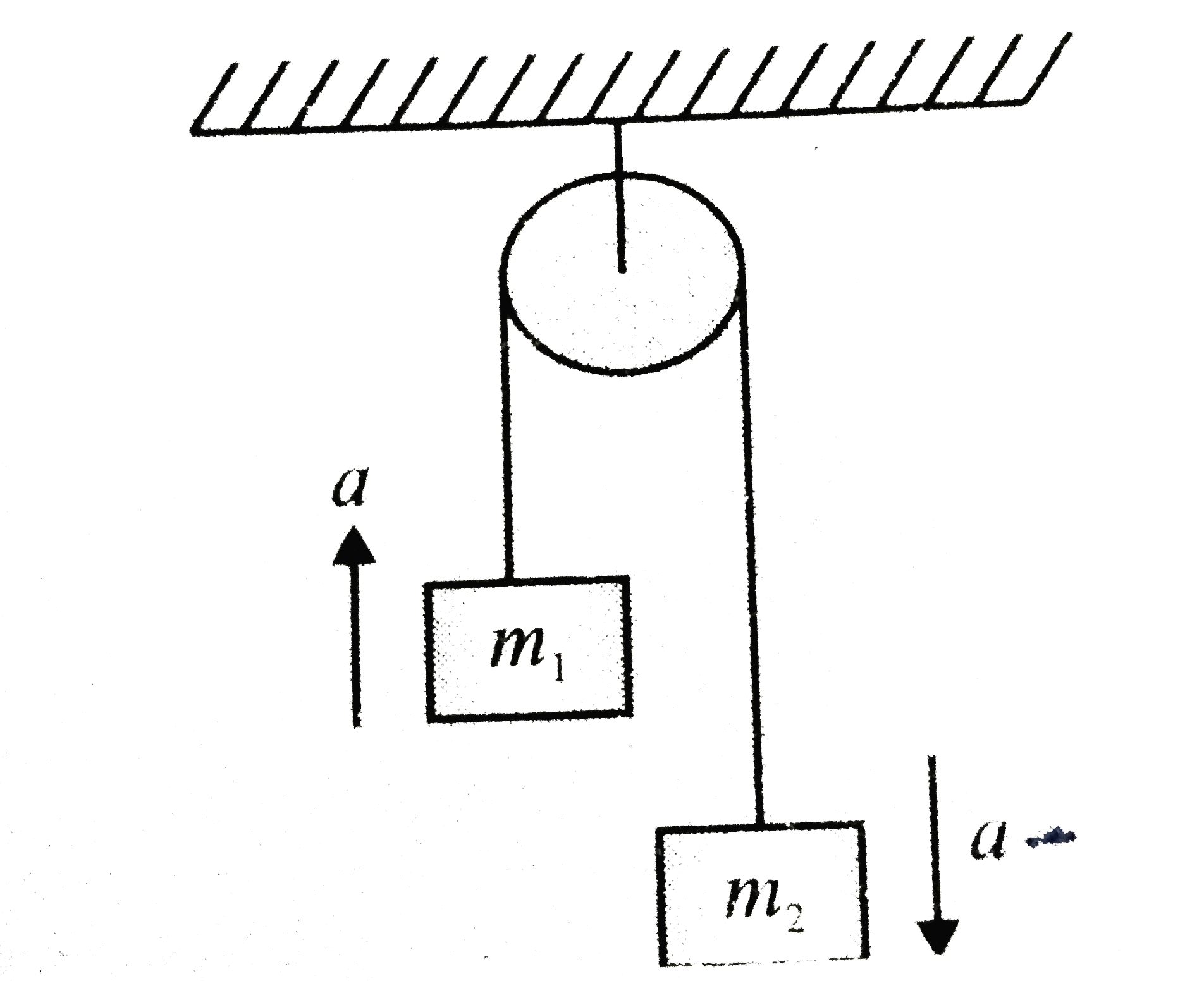
View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
View SolutionA block of mass 'm' is kept on a smooth moving wedge. If the acceleration of the wedge is 'a'
View SolutionA block of mass 2kg slides down the face of a smooth 45∘ wedge of mass 9kg as shown in the figure. The wedge is placed on a frictionless horizontal surface. Determine the acceleration of the wedge.

View SolutionA block of mass m is placed on a smooth wedge of mass M, as shown in the figure . Just after placiing block m over wedge M.
View SolutionA block of mass m is placed on a smooth wedge of inclination Q. The whole system is accelerated horizontally so that the block does not slip on the wedge. Find the
i) Acceleration of the wedge
ii) Force to be applied on the wedge
iii) Force exerted by the wedge on the block.
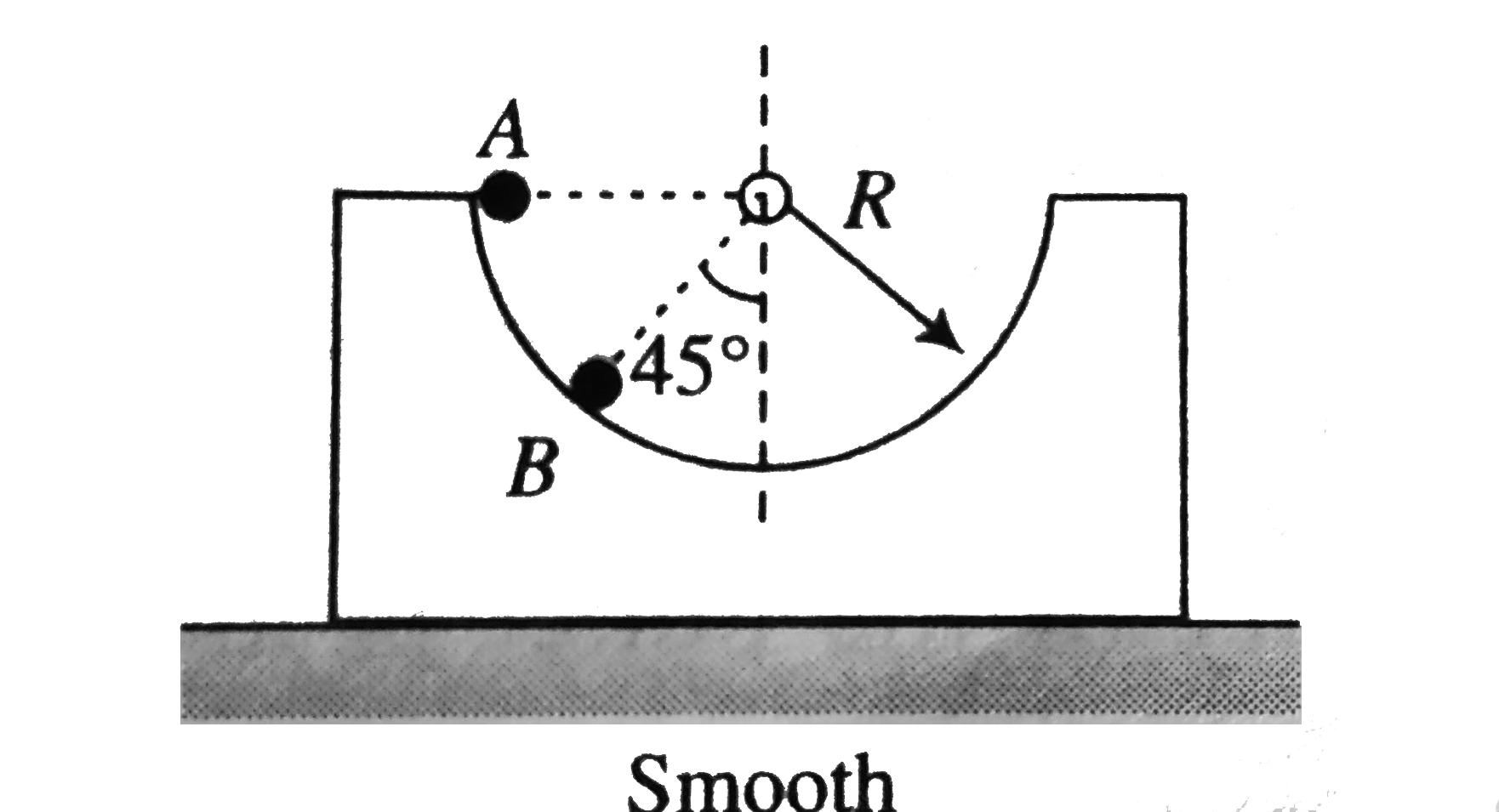
View SolutionA ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
View Solution
