In a ΔABC, I is the incentre and AI cuts BC at D. If B=(-1,2) C(9,7), AB = 14, AC =21 then find D.
The correct Answer is:(3,4)
To find the coordinates of point D where the angle bisector AI intersects side BC in triangle ABC, we can follow these steps:
Step 1: Identify the coordinates of points B and C.
Given:
- B = (-1, 2)
- C = (9, 7)
Step 2: Calculate the lengths of sides AB and AC.
We are given:
- AB = 14
- AC = 21
Step 3: Determine the ratio in which point D divides line segment BC.
According to the angle bisector theorem, the internal angle bisector divides the opposite side in the ratio of the lengths of the other two sides. Hence, we have:
- Ratio of AB to AC = 14:21 = 2:3
Step 4: Use the section formula to find the coordinates of point D.
The section formula states that if a point D divides the line segment joining points B(x1, y1) and C(x2, y2) in the ratio m:n, then the coordinates of D are given by:
D(mx2+nx1m+n,my2+ny1m+n)
Here, m = 2 and n = 3, and we have:
- x1=−1, y1=2 (coordinates of B)
- x2=9, y2=7 (coordinates of C)
Substituting the values into the formula:
Dx=2⋅9+3⋅(−1)2+3=18−35=155=3
Dy=2⋅7+3⋅22+3=14+65=205=4
Step 5: Conclude the coordinates of point D.
Thus, the coordinates of point D are:
D=(3,4)
Given:
- B = (-1, 2)
- C = (9, 7)
We are given:
- AB = 14
- AC = 21
According to the angle bisector theorem, the internal angle bisector divides the opposite side in the ratio of the lengths of the other two sides. Hence, we have:
- Ratio of AB to AC = 14:21 = 2:3
The section formula states that if a point D divides the line segment joining points B(x1, y1) and C(x2, y2) in the ratio m:n, then the coordinates of D are given by:
D(mx2+nx1m+n,my2+ny1m+n)
Here, m = 2 and n = 3, and we have:
- x1=−1, y1=2 (coordinates of B)
- x2=9, y2=7 (coordinates of C)
Dx=2⋅9+3⋅(−1)2+3=18−35=155=3
Dy=2⋅7+3⋅22+3=14+65=205=4
Thus, the coordinates of point D are:
D=(3,4)
Similar Questions
ABC is a triangle and the internal angle bisector of angle A cuts the side BC at D. If A=(3,-5), B(-3,3), C=(-1,-2) then find the length AD
View SolutionIn ΔABC, the perependicular from A BC meets BC at D such that BD=7cmandDC=12cm.Find the ratio of the areas of the triangles ABD and ADC.
View SolutionABC is a triangle right angled at C. If AB=25cmandAC=7cm, find BC.
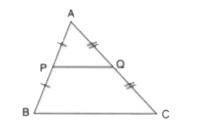
View SolutionIn triangle ABC, P is mid-point of AB and Q is mid-point of AC. If AB = 9.6 cm, BC = 11 cm and AC = 11.2 , find the perimeter of the trapezium PBCQ.
 View Solution
View SolutionIn triangle ABC ,∠B=90∘,AB=40,AC+BC=80, Find :
tan C .View SolutionIf A:B = 2:7 and B:C = 9:13, find A:C.
View SolutionIn triangle ABC ,∠B=90∘,AB=40,AC+BC=80, Find :
sin AView SolutionIn triangle ABC ,∠B=90∘,AB=40,AC+BC=80, Find :
cos AView SolutionIf ABC is a triangle such that A=(1,2) and B=(5,5) with BC=9 and AC =12 units , then slope of altitude CD is (D is a point on BC)
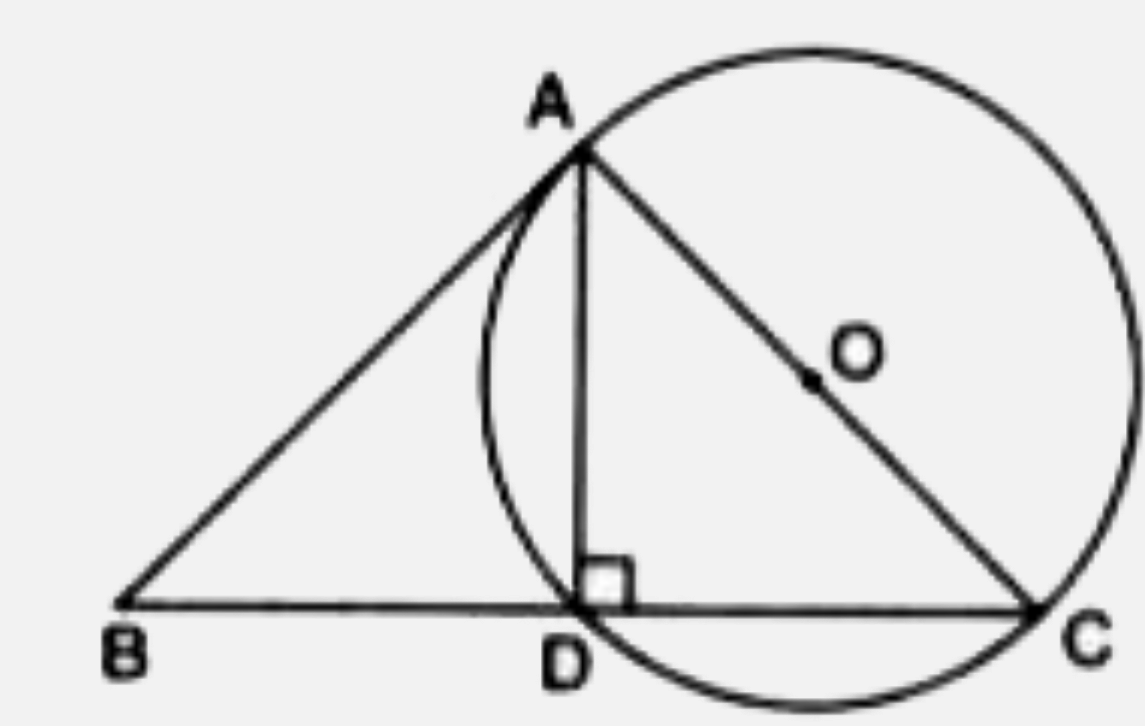
View SolutionThe angle A of the triangle ABC is a right angle. The circle on AC as diameter cuts BC at point D. If BD=9cm and DC = 7 cm, calculate the length of AB.
 View Solution
View Solution
